Keyword Tree
键树(keyword tree),也叫做数字查找树(Digital Search Tree)。
基本介绍
键树,是一棵度的树,树中的每个结点中不是包含一个或几个关键字,而是值含有组成关键字的符号。
如果关键字是数值,那么结点中值包含一个数位; 如果关键字是单词,那么结点中值包含一个字母字符。
这种类型的树,会给某种类型关键字的表的查找带来方便。
| use a table to show an example | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CAI\CAO\LI\LAN\CHA\CHANG\WEN\CHAO\YUN\YANG\LONG\WANG\ZHAO\LIU\WU\CHEN | |||||||||||||||
| CAI\CAO\CHA\CHANG\CHAO\CHEN | LI\LAN\LONG\LIU | WEN\WANG\WU | YUN\YANG | ZHAO | |||||||||||
| CAI\CAO | CHA\CHANG\CHAO\CHEN | LAN | LI\LIU | LONG | WANG | WEN | WU | YANG | YUN | ZHAO | |||||
| CAI | CAO | CHA\CHANG\CHAO | CHEN | LAN | LI | LIU | LONG | WANG | WEN | WU | YANG | YUN | ZHAO | ||
| CAI | CAO | CHA | CHANG | CHAO | CHEN | LAN | LI | LIU | LONG | WANG | WEN | WU | YANG | YUN | ZHAO |
| stop dividing only when each subset contains only one keyword. | |||||||||||||||
由上表的分割过程中,集合、子集、元素之间的层次关系可以用一棵树来表示,这棵树就是键树。上表用下图所示键树来表示。
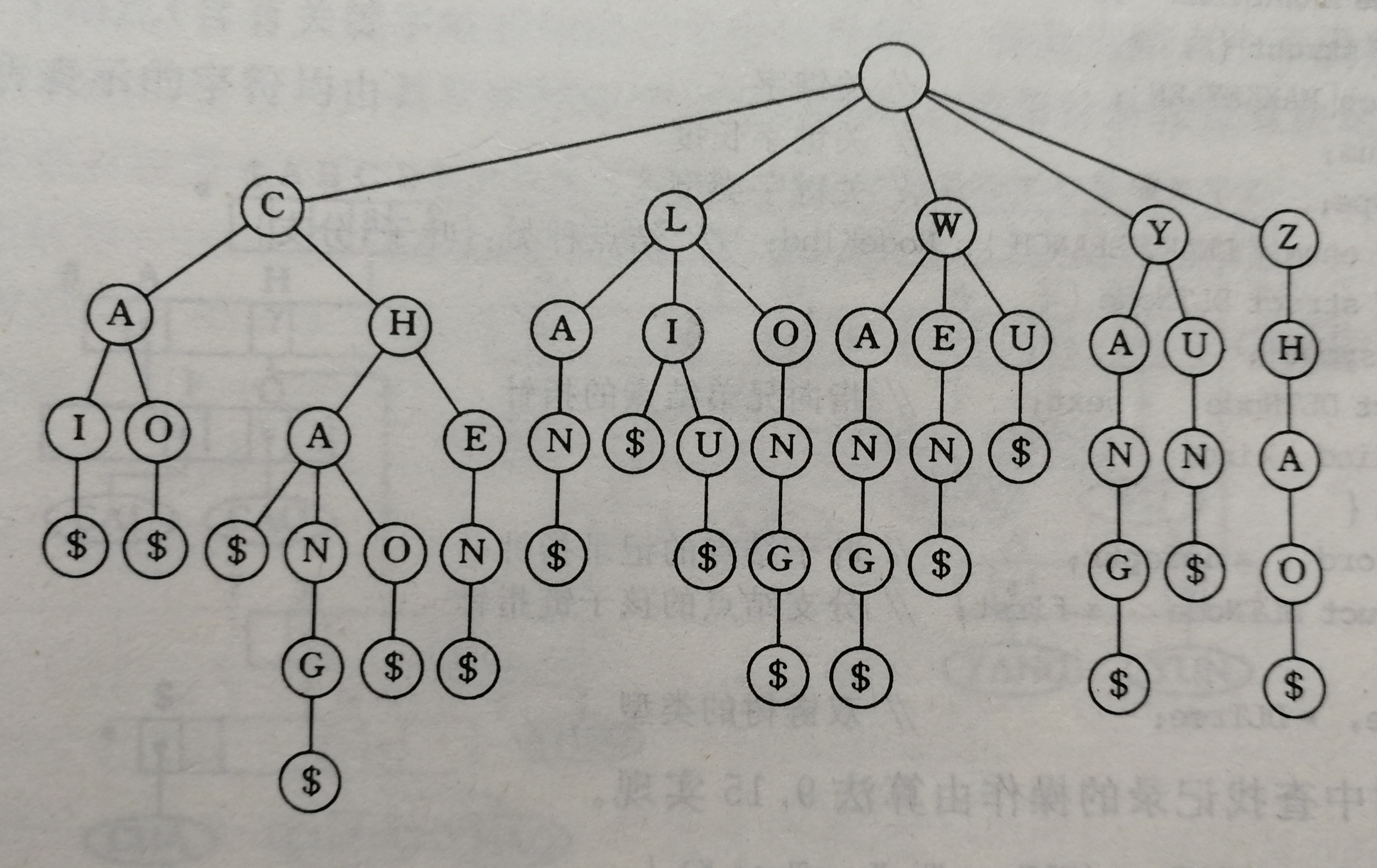
从根到叶结点路径中结点的字符组成的字符串表示一个关键字,叶子中的特殊符号$表示字符串的结束,同时叶结点中含有指向该关键字记录的指针。
为了查找和插入的方便,约定键树为有序树,且结束符$小于任何字符。
两种存储结构
双链树 dst
以树的孩子兄弟链表来表示键树,则每个分支结点包括如下三个域:
| 域 | 内容 |
|---|---|
symbol域 |
存储关键字的一个字符 |
first域 |
存储指向第一棵子树根的指针 |
next域 |
存储指向右兄弟的指针 |
同时,叶结点的inforptr域存储指向该关键字记录的指针。
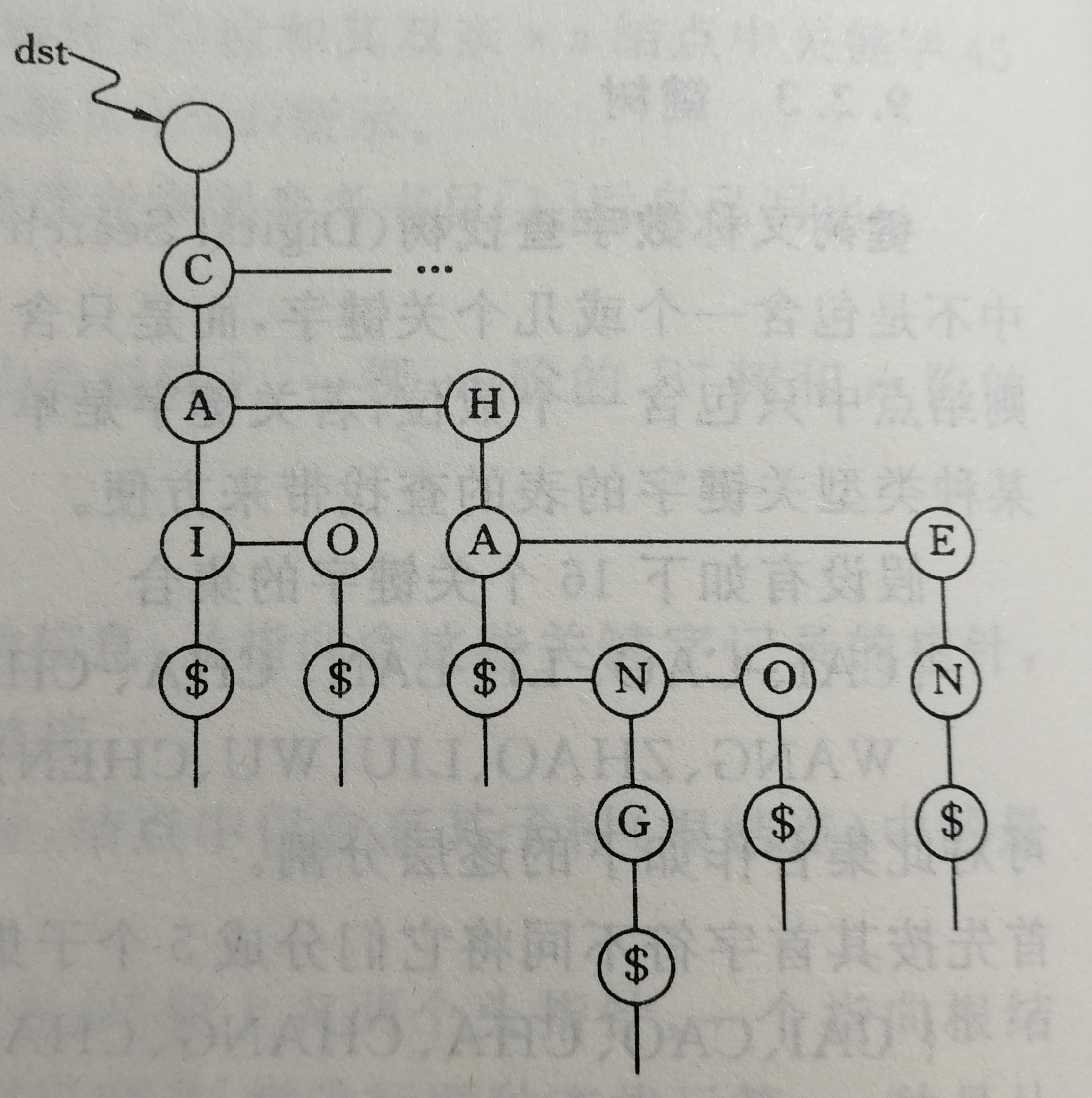
双链树的查找
假设给定值为K.ch,其中K.ch[0]至K.ch[num-2]表示代查关键字中num-1个字符,K.ch[num-1]为结束符$。
从双链树的根指针出发,顺first指针找到第一棵子树的根结点,以K.ch[0]和此结点的symbol域比较,如果相等,则顺first域再比较下一字符,否则沿next域顺序查找。若直到“空”仍比较不等,则查找不成功。
键树中每个结点的最大度d和关键字的“基”有关:如果关键字为单词,则d=27,如果关键字是数值,则d=11. 键树的深度h取决于关键字中字符或者数位的个数。
疑问:为什么字母就26个(假设不分大小写),但是d=27呢?
回答:因为有一个字符$,并且设该字符的序号为0。
假设关键字为随机的,则在双链树中查找每一位的平均查找长度为(1+d)/2;
又假设关键字中字符(或者数位)的个数都相等,则在双链树中的平均查找长度为h(1+d)/2.
插入和删除
相当于在树中的某个结点上插入或者删除一棵子树。
Trie树
用树的多重链表表示键树,每个树的结点中应包含有d个指针域,此时的键树称为Trie树。
trie来自于retrieve(检索)中间四个字符,读音同try。
如果从键树某个结点到叶子结点的路径上每个结点都只有一个孩子,则可将路径上所有的结点压缩成一个"叶子结点",并且在该叶子结点中存储关键字及指向记录的指针等信息。
“可将路径上所有的结点压缩成一个“叶子结点"见图,观察
LIU、LONG、CHANG、CHAO之类。
| 结点类型 | 包含信息 |
|---|---|
| 分支结点 | 含有d个指针域和一个指示该结点中非空指针域的个数的整数域 |
| 叶子结点 | 含有关键字域和和指向记录的指针域 |
分支结点没有数据域,每个分支结点所表示的字符均有其双亲结点中(指向该结点)的指针所在位置决定。
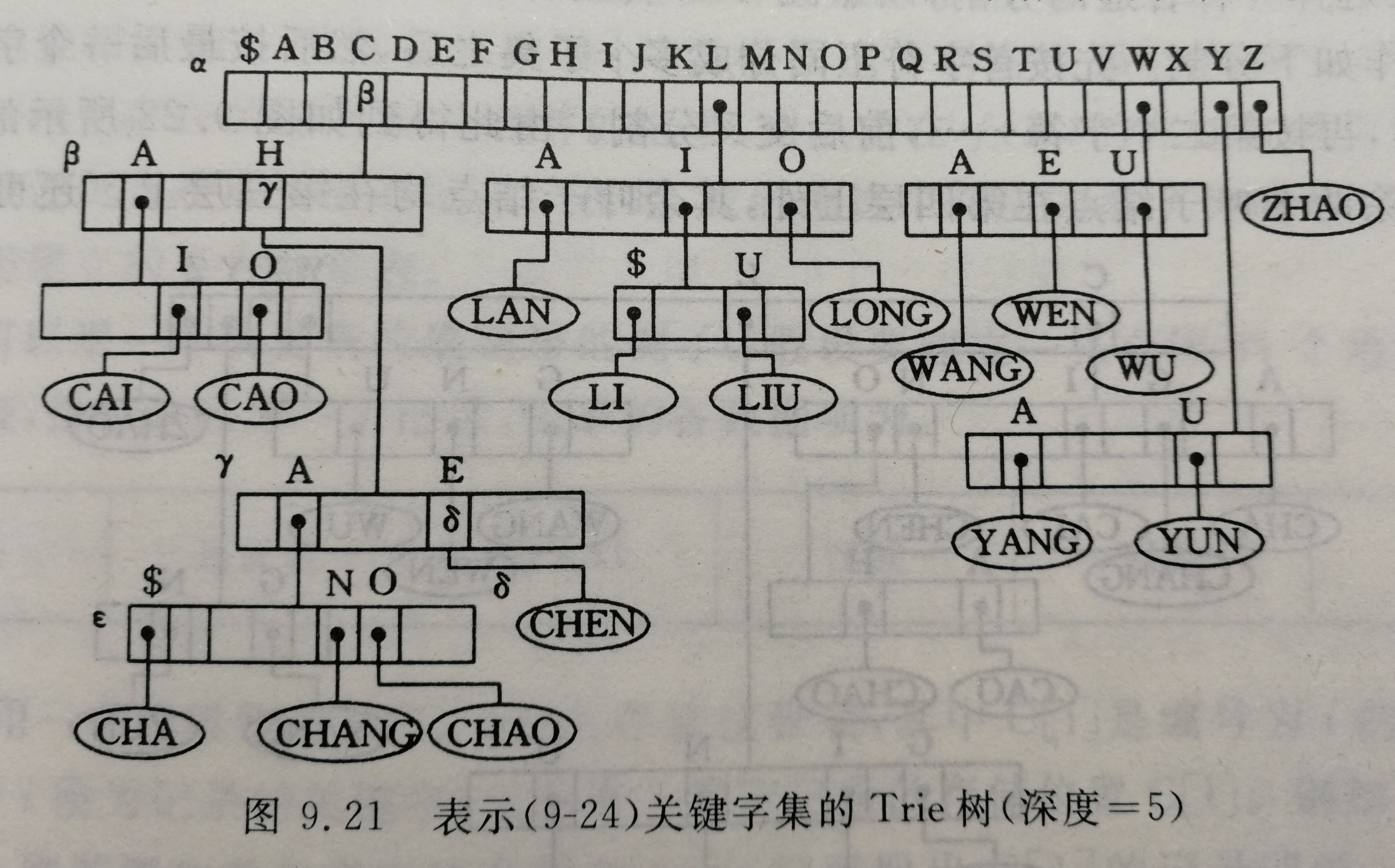
Tire树的查找
从根结点出发,沿和给定值相应的指针逐层向下,直到叶结点。如果叶子结点中的关键字和给定的关键值相等,则查找成功;如果分支结点中和给定值相应的指针为空,或者叶结点中的关键字和给定值不相等,则查找不成功。
Trie树的变化
因为Trie树的查找时间依赖于树的深度。我们可以对关键字集选择一种合适的分割,以缩减Trie树的深度。
下面是一种例子:
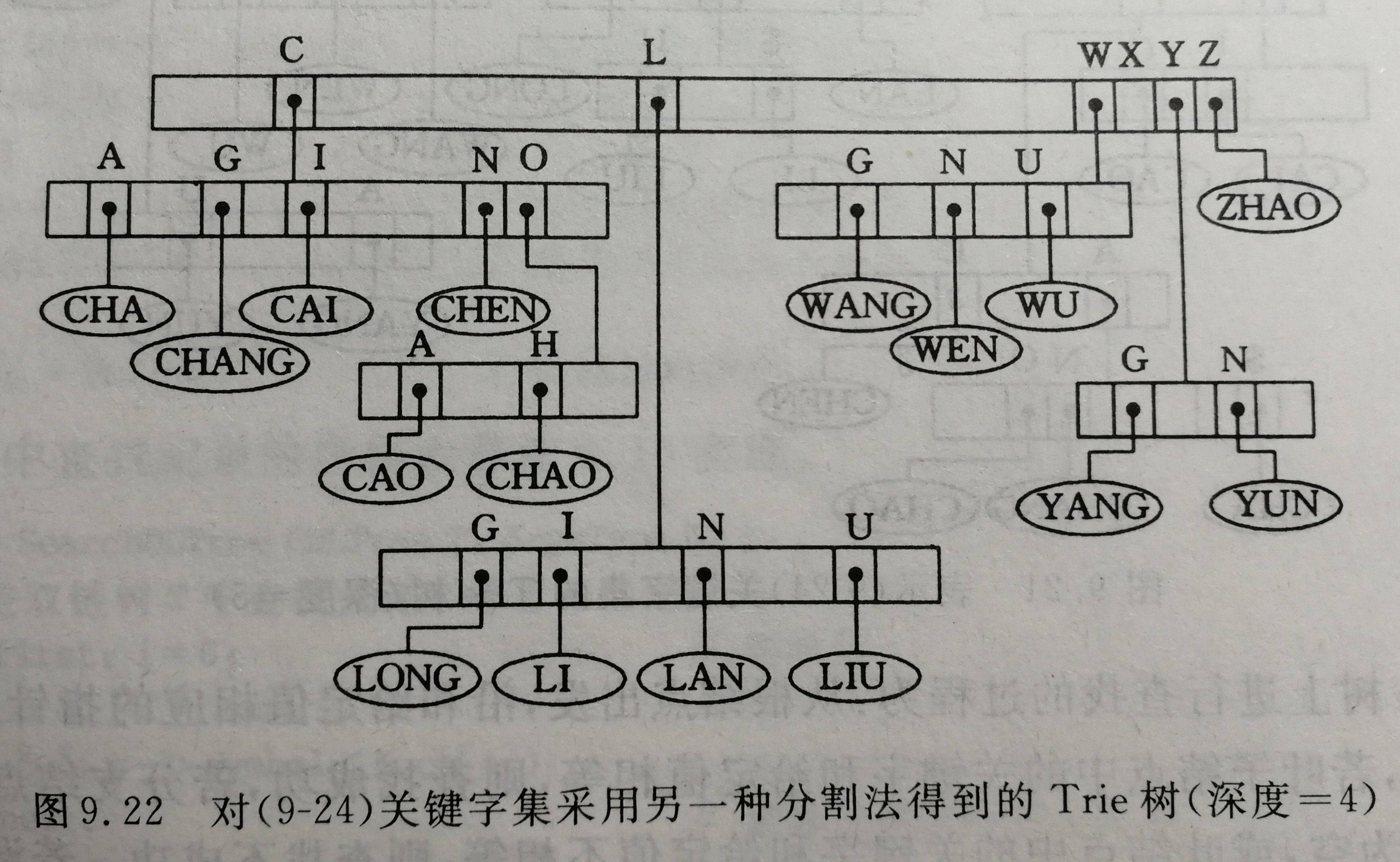
上图中的处理方法:先按首字符不同分为多个子集后,然后按最后一个字符不同分割每个子集,再按照第二个字符…前后交叉分割。
除了上面的处理方法以外,我们同样可以增加分支的个数来减少树的深度。
Trie树上易于进行插入和删除操作(只需要相应的增加或者删除一些分支结点就可以)。如果当分支结点中num域的值减为1的时候,我们就可以把当前分支结点直接删除。
两种存储结构的比较
通过对两种存储结构的了解认识,我们可以发现,如果键树中的结点的度较大时,选用Trie树结构比双链树更加合适。
总结
两种树表的查找过程都是从根结点出发,走了一条从根到叶子(或者非终端结点)的路径,其查找时间依赖于树的深度。
树表主要用于文件索引,因此结点的存取还涉及外部存储设备的特性,故不对他们作平均查找长度的分析。