面向浸没式光刻机的超精密光学干涉式光栅编码器位移测量技术综述
王磊杰, 张鸣, 朱煜, 等. 面向浸没式光刻机的超精密光学干涉式光栅编码器位移测量技术综述[J]. 光学精密工程, 2019, 27(9): 1909-1918.
超精密激光干涉位移测量技术是光刻机实现超微图形高效高保真转移的关键。
相比激光干涉测量技术,平面光栅测量技术凭借极短的光路能够获取极高的环境鲁棒性,从而在实现亚纳米级测量重复性上更具优势。
2. 光栅位移测量传感器基本原理
传统的光栅位移测量传感器 —— 光栅尺是一种利用测量光栅和指示光栅间的莫尔条纹计数原理实现一维线性位移测量的传感器。为了获取足够强度的莫尔条纹,光栅尺的测量光栅和指示光栅节距通常在几十微米量级,故而莫尔条纹型光栅尺的分辨率难以达到纳米量级。此外,莫尔条纹型光栅尺仅能实现一维线性位移测量,所以难以满足多自由度的需求。
于是,新型的光栅位移测量传感器 —— 光学干涉式光栅编码器(或光栅干涉仪)被开发出来,其具备空间多自由度位移测量和纳米甚至亚纳米测量精度的能力。
3. 平面光栅位移测量系统布置方案
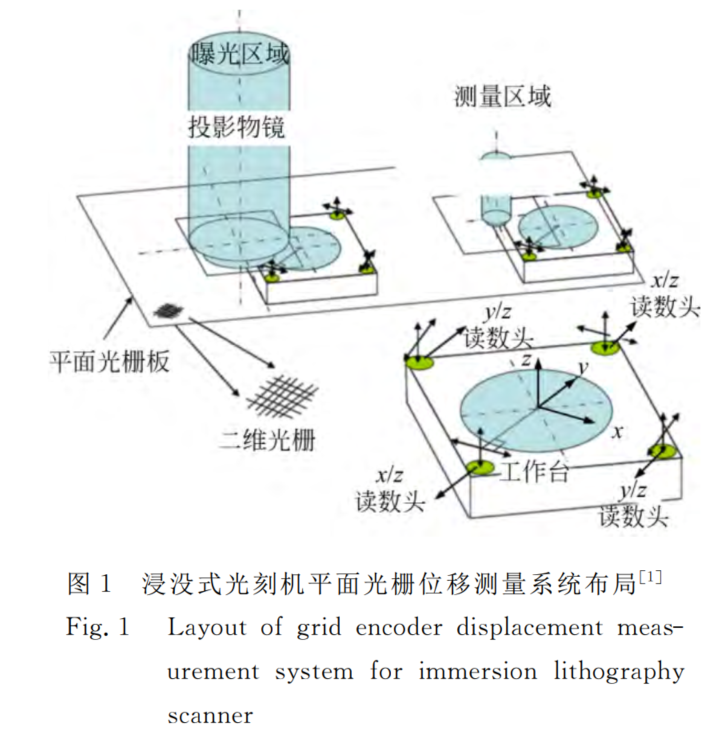
图中为典型的 ASML 光刻机工件台平面光栅位置测量系统布局。工作过程中,最先进的193ArF浸没式步进扫描光刻机工件台需要进行面内大行程(400mm)高速高加速步进($x$)扫描($y$)运动,同时还需要进行约±1mm的垂向调焦运动($z$)和约±1mrad的调平转动($\theta_x/\theta_y/\theta_z$),工件台面内扫描精度需要达到亚纳米级量,步进和垂向运动精度需达到纳米量级。
方案中采用二位光栅作为测量光栅。使用两个能同时实现面内(x)/垂向(z)和面内(y)/垂向(z)位移测量的读数头布置于工件台四角处。4个光栅编码器具有4个面内测量信息和4个面外垂向测量信息,利用8个位移测量信息通过一定的位移解算算法即可得到工件台质心的六自由度位移。
光刻机工件台平面光栅测量系统存在多种方案,但为实现工件台的6自由度位移测量,读数头能够同时测量面内/垂向位移为基本条件。
光刻机工件台的光栅编码器需要满足以下要求:
- 实现面内/垂向位移同时测量;
- 光栅编码器具有大转角允差和离轴允差(确保工件台调平调焦运动过程中保持很高的测量信噪比;
- 测量精度:面内亚纳米级,垂向纳米级;
- 体积小、质量轻、集成性好。
- 干涉信号由共轴光形成,工件台再 ±1 mrad 调平转动($\theta_x/\theta_y/\theta_z$)和 ±1 mm 的垂向调焦运动($z$)时,工件台的光栅编码器的共轴光会产生光斑分离和光束夹角。
- 如果光栅编码器光路方案不能抑制光斑分离和光束夹角,将导致光栅编码器的信号信噪比下降甚至不能工作,故需要保证光栅编码器具有大转角允差和离轴允差。
4. 光栅编码器设计方案
4.1 测量原理
【面内一维线性位移测量原理】利用一维测量光栅的±1级衍射光干涉形成一路干涉测量信号,当光栅沿矢量方向 运 动时,±1级衍射光将发生光栅多普勒效应,从而将位移测量信息写入至干涉信号中,后续通过对干涉信号进行处理即可得到一维位移信息。
【面内二位线性位移测量】利用二维平面光栅实现测量维数扩展。
【面内/垂向二维线性测量原理】
- Kimura等 提出了能够实现面内/垂向二维线性位移同时测量的参考型光栅编码器。基本原理:利用一维测量光栅衍射的±1级衍射光分别与在光栅编码器内部的两路参考光干涉形成两路干涉信号,干涉信号中均包含面内和垂向位移信息;当一维测量光栅沿面内和垂向同时运动时,两路干涉信号中面内位移信息相反,垂向位移信息相同;将两路测量信号相加减即可分别解算出面内和垂向位移信号。
- Guan等 提出了能够实现面内/垂向二维线性位移同时测量的自参考型光栅编码器。基本原理:光栅编码器包 含两个测量模块,测量模块1利用一维测量光栅的正一级衍射光和零级衍射光干涉形成测量信号1,测量模块2则利用一维测量光栅的负一级衍射光和零级衍射光干涉形成测量信号2;当测量光栅沿面内和垂向同时运动时,两路干涉信号中面内位移信息相反,垂向位移信息相同;将两路测量信号相加减即可分别解算出面内和垂向位移信号。
【面向/垂向三维线性测量原理】Kimura等 基于面内/垂向二维线性位移测量原理提出了面内/垂向三维线性测量光栅编码器,即将一维光栅扩展为二维光栅,利用二维光栅衍射的(1,0),(-1,0),(0,1)和(0,-1)4束衍射光分别与光栅编码器内部的4束参考光干涉形成4路干涉信号;4路信号中,两路包含面内(x)和垂向位移测量信息,两路包含面内(y)和 垂向测量信息。对4路位移测量信息进行冗余解算可得到面内/垂向的三维位移。
【三自由度转角测量原理】Saito等 提出了能够实现三自由度转角测量的光栅编码器,即将光栅的+1级、-1级 和0级衍射光通过透镜入射至布置于透镜焦点处的3个二维四象限探测器上,当光栅产生三自由度转角时,将引起3个衍射光斑在二维四象限探测器上运动,二维四象限探测器共输出6个光束移动位移值,利用6个光束移动位移值即可解算出三自由转角值。
【空间六自由度测量原理】Li等 在面内/面外三维测量原理和三自由度转角测量原理的基础上,提出了可实现空间六自由度测量的光栅编码器。
由光刻机工件台的需求可知,光刻机工件台光栅编码器至少能够实现面内/垂向二维测量,文献中的面内/垂向二维、面内/垂向三维和空间六自由度测量原理可以作为光刻机工件台光栅编码器测量原理的参考,但考虑到安装空间的要求,难以直接应用在浸没式光刻机中。
4.2 相位探测方案
现有文献中光栅编码器的相位探测方式可以分为零差探测和外差探测两种类型。
【零差式】零差相位探测采用单频激光形成干涉信号,干涉信号是直流信号,直流信号的抗干扰能力较弱且不易细分,不易实现高精度(需要采用修正算法进行修正);单路直流信号难以实现判向和精度修正,需要增加光学移相光路获取四路正交信号,这将致使编码器光路复杂、器件增加,从而增大集成化和小型化的难度。
【外差式】外差相位探测采用两个频率激光形成拍频信号,拍频信号为交流信号,便于细分和判向,抗干扰能力强,易于实现高测量精度,但测量速度受限于差频激光的频差且存在偏振混叠误差。
外差差频激光产生的方式有以下三种:
- 电光调制器(EOM)
- 塞曼效应
- 声光调制器(AOM)
- 通常EOM 产生的差频激光频差在1kHz左 右,塞曼效应最大产生的频差在5 MHz,AOM 产生的频差在几十 MHz左右。
- 光刻机工件台超精密光栅编码器要求精度达亚纳米级,测量速度达m/s级,故基于 AOM 的外差相位探测方案可作为实现精度和测量速度指标的重要选择。
4.3 分辨率增强光路的方案
光栅编码器的测量信号需要进行细分方能实现亚纳米甚至更高的分辨率。现有文献中光栅编码器的测量信号细分的方法主要有两种:
- 光学细分
- 电子细分(是光栅编码器实现超高分辨率的主要方法,能实现4096甚至更高的细分率)
二次衍射光路是光栅编码器实现4光学细分率的重要方案,即测量光往返于编码器和测量光栅两次,从而实现光学分辨率倍增。
光刻机工件台超精密光栅编码器要求分辨率达到深纳米级,二次衍射光路方案可作为实现深纳米级测量分辨率的重要选择。
4.4 转角/离轴允差光路方案
光栅编码器信号是由共轴光干涉形成的,光栅编码器实际使用时,编码器和光栅之间的转角/离轴允差将导致共轴光位置分离和光束夹角,从而引起测量信号强度和信噪比下降甚至测量信号丢失,进而造成测量精度下降甚至编码器无法工作。
在较大的转角/离轴允差范围内保持很高的测量信号信噪比,是光栅编码器所追求的重要性能。较大的转角/离轴允差可以通过设计光栅编码器的光路方案来实现。
光刻机工件台的光栅编码器要在±1mm 的离轴和±1mrad的转角允差内保持很高的测量信号信噪比。
4.5 死程误差
光栅编码器利用测量光路和参考光路形成干涉信号,由于测量光路和参考光路通常难以共光路而形成死程,环境波动会导致测量误差,即死程误差。
为了降低死程误差和环境控制指标,
- 程方等 采用测量光路非常短且对称的光栅编码器以降低死程误差。
- Wu、Hsieh等 提出了准共光路光栅编码器位移测量系统,以最大程度抑制死程误差,在标准试验室环境下实现了米 级的测量稳定性。
【准共光路方案】利用透镜将光束聚焦至光栅上,光栅产生的衍射光中的零级和正一级发散并发生重叠,将重叠部分利用透镜准直变成平行光实现准共光路设计。
4.6 需要解决的问题
现有原理上可同时测量面内和面外位移的光栅编码器难以直接应用于光刻机工件台中的具体原因:
- 【鲁棒性】现有光栅编码器为零差编码器编码器,抗干扰能力弱,不易实现高精度。
- 现有光栅编码器的光路方案在光栅和编码器存在±1mad转角和±1mm 离轴时,形成干涉信号的共轴光光斑分离和光束夹角非常大
- 【激光利用率】现有光栅编码器的光路方案的激光利用率较低
- 【尺寸】编码器尺寸大、质量较重,不易于实现小型化和集成化
5. 光栅编码器精度
光刻机工件台的光栅编码器需要达到亚纳米级的测量精度。
【周期非线性误差】1)对于零差光栅编码器,通过四路正交测量信号求反正切实现位移求解和判向;由于编码器自身器件的不理想,4路测量信号的直流漂移、交流幅值不等幅和相位不正交将导致在位移求解时产生周期非线性误差;2)对于外差光栅编码器,由于差频激光的偏振和频率混叠,也将导致周期非线性误差(偏振频率混叠误差)。
外差干涉仪的偏振混叠误差建模方法主要有两种,一是数学解析方法,二是数值计算方法(更适用)。
【死程误差】光栅编码器利用测量光路和参考光路形成干涉信号,由于测量光路和参考光路通常难以共光路而形成死程,环境波动导致测量误差,即死程误差。
- 实际上,光栅编码器只要非共光路,环境存在波动,死程误差仍然存在。
- 在双频激光干涉仪死程误差的研究中,采用基于修正Elden 公式的死程误差补偿方法:首先测量出编码器工作空间内诸如温度、湿度、压力梯度等实际平均环境指标值,然后利用 Elden公式根据实际平均环境指标值计算出实际空气折射率,利用实际空气折射率替代标准折射率计算双频激光编码器的实际测量值,从而实现死程误差的补偿。
【几何误差】光栅编码器的光学器件之间的形位公差、光束指向偏差、测量光栅转角/离轴偏差均会引起编码器光路偏离理想光路从而引起几何误差。
【热漂移误差】光学器件受温度波动会发生热膨胀,从而引起光栅编码器的热漂移误差。
Holmes等 针对双频激光编码器的热漂移误差开展了误差静态建模,建立了双频激光编码器的热漂移系数与其器件折射率、尺寸和热膨胀系数之间的静态数学模型,并给出了双频激光编码器的热漂移系数和不确定度,最终根据温度变化计算出了热漂移误差。然而,热漂移误差属于缓慢变化的动态误差,会影响光栅编码器的长期稳定性、重复性和精度;且文献中给出的模型将由多种材料器件组成的编码器的折射率、热膨胀系数近似为一种光学器件的折射率、热膨胀系数,模型不够精确。
【波前畸变误差】光学器件的面型误差、测量光栅转角/离轴偏差引起的光束偏移、空气扰动等因素会引起光束波前畸变。
5.0 实现亚纳米测量精度需解决的问题
总体来说,现有光栅编码器精度方面的研究缺少系统全面的以误差分类表、误差建模方法、误差修正方法和误差分配方法为体系的精度保障机制。
在误差建模方法、误差修正方法及误差分配方法仍以静态误差建模为主且模型不够精确,而实际上光刻机工件台则更为关注于动态误差,且要求达到亚纳米级的极限测量精度,这难以适用于光刻机工件台光栅编码器高动态测量下实现亚纳米测量精度的应用需求。