超精密六自由度微动台耦合动力学建模及分析
蒋毅, 朱煜, 杨开明, 等. 超精密六自由度微动台耦合动力学建模及分析[J]. 中国电机工程学报, 2014, 30.
作为光刻机的关键子系统,工件台的运动性能要求随着社会生产制造需求的提高而快速增长,其中主要包括:
- 大运动行程;
- 高速度;
- 高加速度;
- 高重复定位精度;
- 高轨迹跟踪精度;
- 多自由度运动。
为实现以上运动性能,国内外采用的技术主要有
- 多个直线电机叠层驱动
- 长行程粗运动与短行程微运动相结合的粗精叠层运动(目前被广泛使用)
- 六自由度磁悬浮运动
- 。。。
【粗精叠层运动】粗动台完成大行程微米级的粗运动,微动台完成小行程纳米级的精运动。
光刻机微动台属于一类典型的无接触式六自由度运动台。对于此类多输入多输出(multi-input multi-output,MIMO)运动系统,由于结构柔性、制造误差以及安装误差等因素,系统内部耦合成为实现高伺服性能的主要障碍之一。
造成系统耦合的因素有很多种,其中主要体现为 2 类耦合:
- 【位置相关耦合】控制点和电机力分配点不重合
- 【力相关耦合】电机力分配不合理
【过驱动系统】输入(电机数)多于输出(自由度),需要添加适当的约束条件以实现合理的力分配方式。
对于【冗余输入】,学者们提出了多种分配方式。
- 采用基于电流二范数最小的广义逆来得到分配方案
- 采用单向电机来控制转角
这两种方案均会导致电流分配不均,造成局部过热等问题。
力转换模型主要推导过程
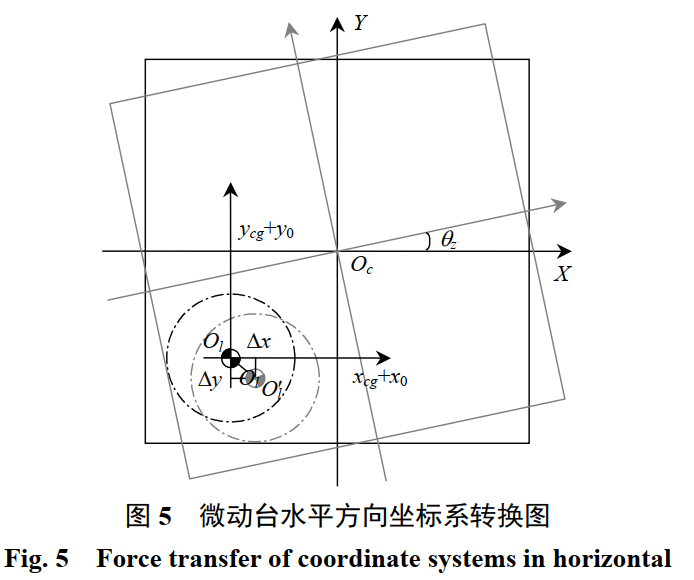
- 初始状态下微动台质心在测量坐标系下坐标为 $(x_0,y_0,z_0)$
- 测量坐标系下,测量值为 $(x_l,y_l,z_l,\theta_x,\theta_y,\theta_z)$
- 质心位移量 $x_{cg},y_{cg}$
- 解算点位移量 $x_l,y_l$
- $\theta_z$为绕质心 $O_C$ 的旋转量,$\theta_z$ 会造成解算点 $O_l$处的附加位移增量 $(\Delta x,\Delta y)$,这就是位置相关耦合产生的原因。
.PNG)