子空间分析与跟踪(6) —— 快速子空间分解
先知道
Krylov 方法$^{[2]}$
Krylov方法是一种“降维打击”手段。特点有二:牺牲了精度换取了速度;在没有办法求解大型系数矩阵时,给出了一种方法。
在处理线性方程组的求解问题(求解未知向量 $x$)
\[Ax=b\]一般做法为直接求矩阵 $A$ 的逆 $A^{-1}$ 然后可得
\[x=A^{-1}b\]但如果 $A$ 的维度很高,甚至是一个稀疏矩阵,我们就需要用一种方法来替换 $A^{-1}$
\[A^{-1}b\approx\sum_{i=0}^{m-1}\beta_iA^ib\]其中 $\beta$ 都是未知标量,$m$ 是我们假设的一个值,最大不能超过矩阵的维度。
至于为什么可以用这种方法来替换 $A^{-1}$ 是因为 Cayley–Hamilton 定理,详情可以见 维基百科中哈密尔顿–凯莱定理的例子部分。$^{[3]}$
解 $\beta$ 的值需要我们将替换的东西带入式子 $Ax=b$ 得到
\[0=b-Ax^{(m)}=b-A\sum_{i=0}^{m-1}\beta_iA^ib\]因为未知标量 $\beta$ 的个数 $m$ 不能超过矩阵的维度,故而上面的这个方程组中方程数大于未知数的个数。此种情况只能求近似解,而此方程组为线性,所以我们可以使用最小二乘法。
首先设一个(不想要的或者说想要尽可能小的东西)残量(error) $r^{(m)}=b-Ax^{(m)}$ ,将该求近似解的问题转化为一个最优化问题。
而最小二乘法的核心就是:
\[\begin{matrix} \frac{\partial r}{\partial\beta_i}=0,&i=0,1,...,m-1 \end{matrix}\]其中 $r=\sum_{i=1}^{n}(r_{i}^{(m)})^2$
快速子空间分解的算法的基本出发点
样本协方差矩阵 $\hat{R}$ 的主特征向量的张成与 $\hat{R}$ 的Rayleigh-Ritz(RR)向量的张成是 $R$ 的信号子空间的渐进等价估计。由于RR向量可以利用Lanczos算法有效求出,故可以实现信号子空间的快速分解。
Rayleigh-Ritz逼近
Hermitian矩阵的特征值分解
Hermitian矩阵 $A$ 的特征值分解如下
\[A=\sum_{k=1}^{M}\lambda_ku_ku_k^H\]其中,$(\lambda_k,u_k)$ 为 $A$ 的第 $k$ 个特征值和特征向量,并假定 $\lambda_1>…>\lambda_d>\lambda_{d+1}=…=\lambda_{M}=\sigma$。这就说明,${\lambda_k,u_k}$ 为信号特征值和信号特征向量。
对于矩阵特征对(特征值、特征向量)的理解我们可以看一下马同学的知乎专栏:如何理解矩阵特征值和特征向量?。
Rayleigh-Ritz值,Rayleigh-Ritz向量

几何的角度来看,向量之差与子空间正交,而正交可以使得影响最小。
Krylov子空间

Rayleigh-Ritz逼近

推导过程:对于式子 $Q^HAQu_i=\alpha_iu_i$ 两边同时左乘矩阵 $Q$ 即可。
逼近的评估方法
看差值的收敛速度


快速子空间分解算法
Lanczos基
$Q$ 为子空间的某一正交基,也称为 Lanczos基,
\[Q=[q_1,q_2,...,q_m]\]快速子空间分解算法的主要思想
Lanczos基 可以通过将Hermitian矩阵三对角化,将 $A$ 的RR对(RR值和RR向量)与三角矩阵的特征对(特征值和特征向量)紧密联系在一起。
\[Q^H_m\hat{A}Q_m=T_m=\begin{bmatrix} \alpha_1&\beta_1&&&\\ \beta_1&\alpha_2&\beta_2&&\\ &...&...&...&\\ &&...&\alpha_{m-1}&\beta_{m-1}\\ &&&\beta_{m-1}&\alpha_{m}\\ \end{bmatrix}\]其中,$T_m$ 称为 $m\times m$ 实三对角矩阵。
Lanczos算法
Lanczos算法有两种:
- 实现Hermitian矩阵的三对角化的三Lanczos迭代;
- 实现任意矩阵双对角化的双Lanczos迭代。
两种方法可以相互转换。
关于RR逼近

- "结构化的矩阵"
三Lanczos迭代算法

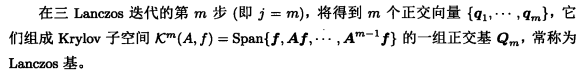
快速子空间分解算法(三Lanczos迭代)


双Lanczos迭代

"对数据矩阵 $X_N$ 使用双Lanczos迭代"与"对样本协方差矩阵 $\hat{A}$ 使用三Lanczos迭代"的等价性

快速子空间分解算法(双Lanczos迭代)


参考
[1] 张贤达. (2004). 矩阵分析与应用. 清华大学出版社有限公司.
[2] 陈与论. (2016, November 23). 如何使用Krylov方法求解矩阵的运算尤其是逆? Retrieved February 16, 2022, from 知乎: https://www.zhihu.com/question/23309010/answer/73365393
[3] 哈密尔顿–凯莱定理 Retrieved February 16, 2022, from 维基百科: https://zh.wikipedia.org/wiki/%E5%87%B1%E8%90%8A%E2%80%93%E5%93%88%E5%AF%86%E9%A0%93%E5%AE%9A%E7%90%86
[4] 马同学. 如何理解矩阵特征值和特征向量? Retrieved February 16, 2022, from 知乎: https://www.matongxue.com/madocs/228/