数字信号处理相关知识(1)
信号
信号分为连续时间信号和离散时间信号,通常以t表示连续时间变量,以n表示离散时间变量,计算机只能处理离散时间信号,通过之后的学习了解到,基于采样定理我们可以先把一个连续时间信号变换成离散时间信号,然后利用计算机来处理离散时间信号,最后再把它变换回连续时间系统中,简称C/D转换和D/C转换。
单位冲激和单位跃阶是两个最基本的信号,其他信号可以利用单位冲激信号来构成和表示。
系统
系统可以理解为信号处理的过程。
- 处理连续时间信号的就是连续时间系统;
- 处理离散时间信号的就是离散时间系统。
【线性时不变系统】有一个很好的性质是叠加性。
线性时不变系统
一般信号都可以表示成单位冲激信号的线性组合,根据叠加性质和时不变性,我们能够用线性时不变系 统的单位冲激响应来表征任意一个线性时不变系统的特性。
- 离散时间的线性时不变系统的响应可以用卷积和来表示,
- 连续时间的线性时不变系统的响应可以用卷积积分来表示。
用线性常系数微分方程来描述连续时间系统,用线性常系数差分方程来描述离散时间系统。
【初始松弛条件】初始松弛是一种对信号的初始条件的描述。如果说一个累加器在n之前没有激励,那么初始条件就是:当n<0时,y(n)=0.这种情况就是初始松弛。满足初始松弛条件系统的响应时,是等同零状态响应。
周期信号的傅里叶级数表示
因为一个复指数信号的响应仍然是一个复指数信号,不同的只是幅度上的变化,所以将周期信号表示成傅立叶级数可以让它更便于分析。
若 $x(t)=e^{st}$,那么系统对$x(t)$的响应$y(t)$为:
\[y(t)=H(s)e^{st},~while~H(s)=\int_{-\infty}^\infty h(\tau)e^{-s\tau}\]若一个连续时间系统的输入可以表示成复指数的线性组合
\[x(t)=\sum_k a_ke^{s_kt}\Rightarrow y(t)=\sum_k a_kH(s_k)e^{s_kt}\]对于连续时间周期信号来说,若它满足狄利克雷条件,则可以用傅里叶级数表示(而自然界中大多数信号都是满足狄利克雷条件的)。在不连续点会产生吉布斯现象,呈现高频起伏和超量。
【吉布斯现象】在工程应用时常用有限正弦项正弦波叠加逼近原周期信号。所用的谐波次数N的大小决定逼近原波形的程度,N增加,逼近的精度不断改善。但是由于对于具有不连续点的周期信号会发生一种现象:当选取的傅里叶级数的项数N增加时,合成的波形虽然更逼近原函数,但在不连续点附近会出现一个固定高度的过冲,N越大,过冲的最大值越靠近不连续点,但其峰值并不下降,而是大约等于原函数在不连续点处跳变值的9%,且在不连续点两侧呈现衰减振荡的形式。

周期连续信号的傅里叶级数:
\[x(t)=\sum_{k=-\infty}^{+\infty} a_ke^{jk\omega_0t},\textbf{ while } a_k=\frac{1}{T}\int_Tx(t)e^{-jk\omega_0t}dt\]周期离散信号的傅里叶级数(DFT):
\[x[n]=\sum_{k=<N>}a_ke^{jk\omega_0},\textbf{ while } a_k=\frac{1}{N}\sum_{k=<N>}x[n]e^{-jk\omega_0n}\]因为DFT的计算量非常巨大,利用DFT的周期性、对称型和正交性,我们可以使用快速傅里叶变换(FFT),使得计算量大大降低。
滤波
滤波用于改变一个信号中各频率分量的相对大小,用于改变频谱形状的线性时不变系统被称为频率成形滤波器,而通过某些频率,显著的衰减掉另一些频率的系统被称为频率选择性滤波。
无源滤波器按所通过信号的频段可分为低通、高通、带通、带阻和全通滤波器五种:
- 低通滤波器:它允许信号中的低频或直流分量通过,抑制高频分量或干扰和噪声;
- 高通滤波器:它允许信号中的高频分量通过,抑制低频或直流分量;
- 带通滤波器:它允许一定频段的信号通过,抑制低于或高于该频段的信号、干扰和噪声;
- 带阻滤波器:它抑制一定频段内的信号,允许该频段以外的信号通过,又称为陷波滤波器。
- 全通滤波器:全通滤波器是指在全频带范围内,信号的幅值不会改变,也就是全频带内幅值增益恒等于1。一般全通滤波器用于移相,也就是说,对输入信号的相位进行改变,理想情况是相移与频率成正比,相当于一个时间延时系统。
连续时间的傅里叶变换
非周期信号也可以用复指数的线性组合来表示。非周期信号可以看成频率无限小(或者是周期无限长)的周期信号,
在一个周期信号的傅立叶级数表示中,当周期增加时,基波频率就会减小,当周期趋于无穷大时,成谐波关系的各分量在频率上就是连续的,傅立叶级数的求和也就变成了积分。
\[x(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}X(j\omega)e^{j\omega t}d\omega\\ X(j\omega)=\int_{-\infty}^{\infty}x(t)e^{-j\omega t}dt\]其中,$X(j\omega)$称为$x(t)$的频域,告诉我们将$x(t)$表示为不同频率正弦信号的线性组合所需要的信息。
当然周期信号也可以建立傅里叶变换。
将周期和非周期放在同一框架内考虑自然是极好的。
连续时间傅里叶变换的微分与积分性质
傅里叶变换的微分与积分性质,再求解常微分方程上很有帮助。
\[\begin{aligned} \frac{dx(t)}{dt}&\Leftrightarrow^\mathcal{F}j\omega X(j\omega)\\ \int_{-\infty}^tx(\tau)d\tau&\Leftrightarrow^\mathcal{F}\frac{1}{j\omega}X(j\omega)+\pi X(0)\sigma(\omega) \end{aligned}\]连续时间傅里叶变换的卷积性质
两个傅里叶信号的卷积映射为其傅里叶变换的乘积,时域的卷积对应频域的乘积。
单位冲激响应的傅里叶变换$H(j\omega)$控制每一频率输入傅里叶变换振幅的变化,可以通过这一性质来衰减一些频率分量的同时保留另一些频率分量。
相对地,时域的相乘对应着频域的卷积。
离散时间的傅里叶变换
离散时间的傅里叶变换和连续时间的傅里叶变换很相似。
\[\begin{aligned} x[n]&=\frac{1}{2\pi}\int_{2\pi}X(j\omega)e^{j\omega n}d\omega\\ X(e^{j\omega})&=\sum_{n=-\infty}^{+\infty}x[n]e^{-j\omega n} \end{aligned}\]$X[j\omega]$称为$x[n]$的频谱,描述了$x[n]$是怎样由这些不同的频率的复指数序列组成。
离散周期信号的傅里叶变换
\[x[n]=\sum_{k=\langle N\rangle}a_ke^{jk\frac{2\pi}{N}n} X(e^{j\omega})=\sum_{-\infty}^{+\infty}2\pi a_k\delta(\omega-\frac{2\pi k}{N})\]离散傅里叶变换的卷积性质
\[\begin{aligned} y[n]&=x[n]\ast h[n]\\ Y(e^{j\omega})&=X(e^{j\omega})H(e^{j\omega}) \end{aligned}\]离散傅里叶变换相乘性质
\[\begin{aligned} y[n]&=x_1[n]x_2[n]\\ Y(e^{j\omega})&=\frac{1}{2\pi}\int_{2\pi}X_1(e^{j\theta})X_2(e^{j(\omega-\theta)})d\theta\\&=\frac{1}{2\pi}X_1(ej\omega)\ast X_2(j\omega) \end{aligned}\]所“离散”,是对于时域而言,而频域一直都是连续的,故而此处频域的卷积仍为积分形式。
信号与系统的时域和频域特性
傅里叶变换时复数值,我们可以用模-相位表示:
- 模描述的是组成$x(t)$的各复指数信号相对振幅信息;
- 相位角不影响各个频率分量的大小,提供的是有关这些复指数信号的相对相位信息。一般来说,相位函数的变化会导致$x(t)$的时域特性的改变。
对于一个频率响应为$H(j\omega)$线性时不变系统,
\[输出的傅里叶变换的模=输入傅里叶变换的模\times频率响应的模,\]同时在输入相位的基础上增加了一个相位。
对于傅里叶变换的模而言,我们通常用对数尺度来描述:
一般采用的对数标尺是以 20 为单位,称为分贝。
由线性常微分方程描述的线性时不变系统在实际中很有用,很多物理系统都可以用这样的方程来建模,而且容易实现,而高阶系统可以由一阶和二阶系统通过级联或并联的形式来实现,因此理解一阶和二阶系统的时域和频域特性非常重要。
采样定律
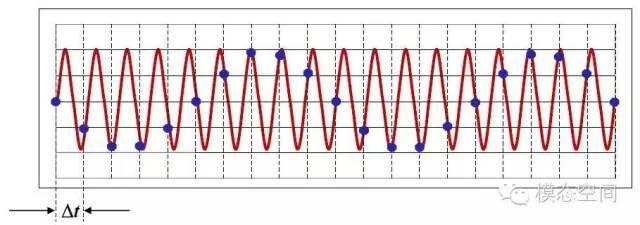
【采样定律】在一定条件下,一个连续时间信号完全可以用该信号在等时间间隔点上的样本来表示,并且通过这些样本值可以把该信号全部恢复出来。
它建立起了连续时间信号和离散时间信号之间的联系。利用采样先把一个连续时间信号变换为一个离散时间信号,再用一个离散时间系统对该信号进行处理,最后再把它变换回连续时间中。
采样频率fs至少为关心的信号最高频率的2倍。采样频率的一半称为奈奎斯特频率。采样频率的一半也称为分析带宽,或简称为带宽。
采样频率必须大于 2 ,被称为奈奎斯特频率,然后通过一个理想低通滤波器就可以恢复到连续时间。如果 采样频率小于2 的话,会产生混叠。
[1] lovelyfrog. 数字信号处理知识总结. Retrieved from http://lovelyfrog.github.io/2018/07/04/signal_and_system_summary/
[2] 维基百科. 吉布斯现象. Retrieved from https://zh.wikipedia.org/wiki/%E5%90%89%E5%B8%83%E6%96%AF%E7%8E%B0%E8%B1%A1
[3] linmue-谭祥军. 采样定理为2倍,为什么经常用2.56倍进行采样?. Retrieved from https://zhuanlan.zhihu.com/p/22480177