十种常见的激活函数 Activation Functions
简单介绍
激活函数是一种添加到人工神经网络中的函数,旨在帮助网络学习数据中的复杂模式。类似人类大脑中基于神经元的模型,激活函数最终决定了要发射给下一个神经元的内容。
在人工神经网络中,一个节点的激活函数定义了一个该节点在给定的输入或者输入集合下面的输出。因此激活函数是确定神经网络输出的数学方程式。
人工神经元的工作原理以及数学可视化过程如下。
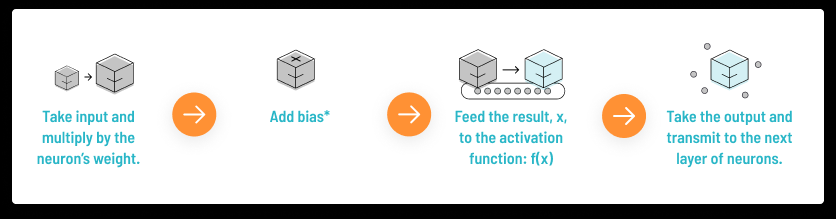
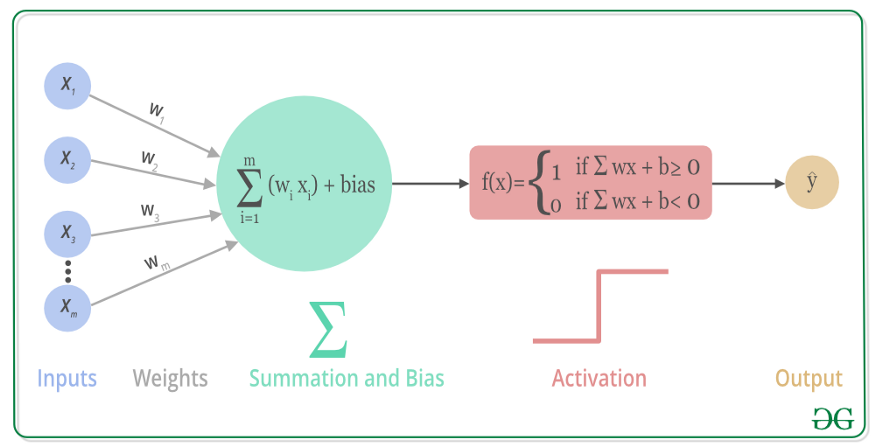
不同种类的激活函数
下面是我自己一些不成熟的大致分类,以便于记忆,见笑了。
"S"形
- sigmoid
- $\tanh$
1. Sigmoid
\[f(z)=\frac{1}{1+e^{-z}}\]适用情况:
- 函数输出范围为0~1,相当于对每个盛景园的输出进行了归一化,故而此激活函数也非常适合将预测概率作为输出的模型。
- 梯度平滑,避免了跳跃的输出值。
缺点:
- 倾向于梯度消失;
- 函数输出不以0为中心,这会降低权重更新的效率;
- Sigmoid函数执行指数运算,时间开销会大一些。
为什么函数输出不以0为中心,权重更新效率会下降?【关于指数运算】但凡激活函数中如果出现指数函数,在时间开销上都会比一般的线性函数要大一些。
2. $\tanh$(双曲正切)
\[f(x)=\frac{2}{1+e^{-2x}}-1\]- 输入较大或者较小时,输出几乎是平滑的的而且梯度较小,这不利于权重的更新;
- 负输入被映射为负,零输入被映射为0(保留本身的正负性)。
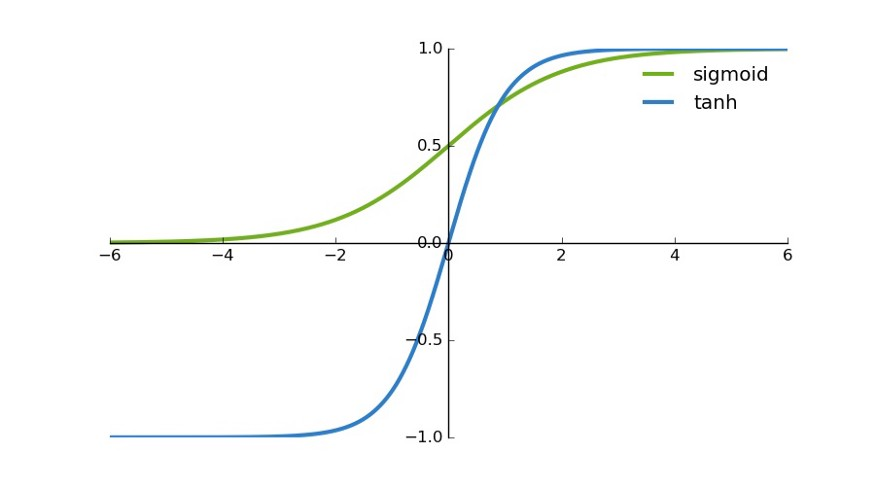
sigmoid vs tanh
- sigmoid和tanh的区别:tanh的输出间隔为1,并且整个函数的以0为中心,权重更新效率比sigmoid好。
一般的二元分类问题中,tanh函数用于隐藏层,而sigmoid函数用于输出层。但这并不固定,需要具体问题具体分析。
"ReLU" 类
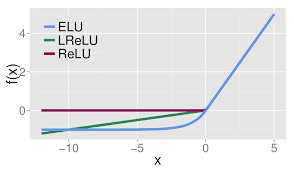
- ReLU
- Leaky ReLU
- ELU
- PReLU
- Softplus
理论上说,Leaky ReLU 以及 ELU 拥有 ReLU 的所有优点,且不会有 Dead ReLU 的问题,但是在实际操作中,尚未完全证明前两者总比 ReLU 好。
3. ReLU (Rectified Linear Unit)
\[\sigma(x)=\begin{cases} \max(0,x),& x\ge 0\\ 0,&x<0 \end{cases}\]相比于sigmoid和tanh函数的优点:
- 输入为正时,不存在梯度饱和的问题;
- 因为此函数只存在线性关系,故而计算速度快很多。
缺点:
- 输入为负时,ReLU完全失效,在正向传播过程中这并不是问题,但在反向传播过程中,如果输入为负数,则梯度完全为零(Dead ReLU 问题);
- ReLU 不以 0 为中心。
Dead ReLU Problem出现的主要原因:1)学习率 $\eta$ 太大导致参数更新幅度太大;2)糟糕的权重初始化。
4. Leaky ReLU
\[f(x)=\begin{cases} x, & x\ge 0\\ ax, & x\le 0 \end{cases}\]- Leaky ReLU 通过将 x 的非常小的曲线分量(ax)基于负输入来调节(ReLU中的)负值的零梯度问题。
- Leaky ReLU有助于扩大 ReLU 函数范围,a 通常为0.01左右。
5. ELU (Exponential Linear Units)
\[ELU(x)=\begin{cases} x, &x\ge 0\\ a(e^x-1),&x<0 \end{cases}\]- 与 ReLU 相比,ELU有负值,这回事激活函数的平均值接近于零,均值激活接近于零可以使学习更快,因为它们使梯度更接近自然梯度。
- ELU 通过减少偏量偏移的影响,使正常梯度更接近于单位自然梯度,从而使均值向零加速学习;
- ELU 在较小的输入下会饱和至负值,从而减少前向传播的变异和信息。
- 分母出现指数运算,计算开销变大。
自然梯度在标准梯度中下降中,我们利用梯度方向上的参数,通过“一小段距离”的位移来训练我们的网络。但是,在定义“小距离”时,我们将其定义为参数空间中的欧氏距离。而欧式距离有一个特点就是它的大小和参数的数量有关:对于两个参数$a,b$的情况,欧氏距离定义为$\text{distance}=\sqrt{a^2+b^2}$。但根据参数的多少来定义“距离”并不总是正确。这就是自然梯度提出原因,预期平等地对待每个参数的变化,不如根据每个参数的变化对我们网络的整个输出分布的影响程度来衡量它。
自然梯度的定义基于KL散度。对于五个参数的网络,度量矩阵为5*5的矩阵(度量矩阵为单位矩阵时此距离定义与欧几里得距离一致)。对于非单位矩阵,我们利用Fisher Information Matrix 作为度规,度量两者之间的距离。而Fisher Information Matrix 为KL散度的二阶导数。
6. PReLU(Parametric ReLU)
\[f(x)=\begin{cases} x,& x\ge x\\ ax, & x<0 \end{cases}\]优点:
- 负值域,PReLU 的斜率较小,可避免 Dead ReLU Problem;
- 与 ELU 相比,PReLU 在负值域为线性运算,尽管斜率很小,但不会趋于零。
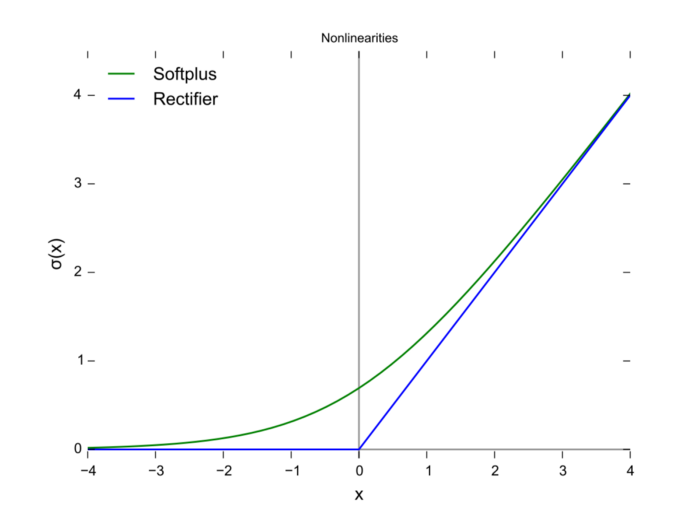
7. Softplus
\[f(x)=\ln(1+e^x)\]也成为logistic函数,与ReLU相似,但相对较平滑。和ReLU一样单侧抑制,其接受范围广。
Others
8. Softmax
该激活函数一般用于多类分类问题的激活函数。在多类分类问题中,超过两个类标签则需要包含类成员之间的关系。对于长度为K的任意实向量,Softmax可以将其压缩为长度为K、值在(0,1)范围内,并且向量总和为1的实向量。
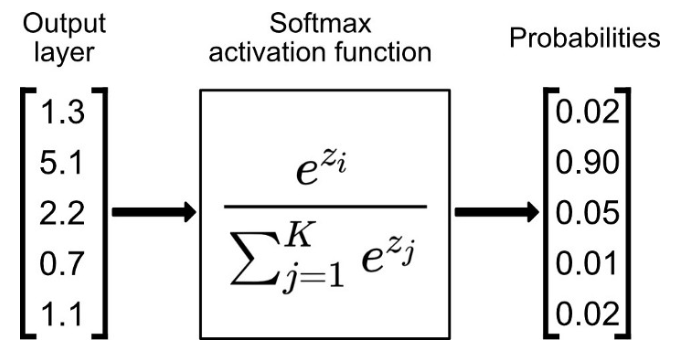
Softmax 与 max 的区别在于其不会丢弃具有较小概率的较小值,他是 argmax 函数的概率版本或者 soft 版本。
Softmax 函数的分母结合了原始输出值的所有因子,这意味着 Softmax 函数获得的各种概率彼此相关。
缺点:
- 零点不可微
- 负输入的梯度为零,这意味着对于该区域的激活,权重不会在反向传播期间更新,因此会产生用不激活的死亡神经元。
为什么该激活函数负输入的梯度为零?
9. Swish
\[y = x * \text{sigmoid} (x)\]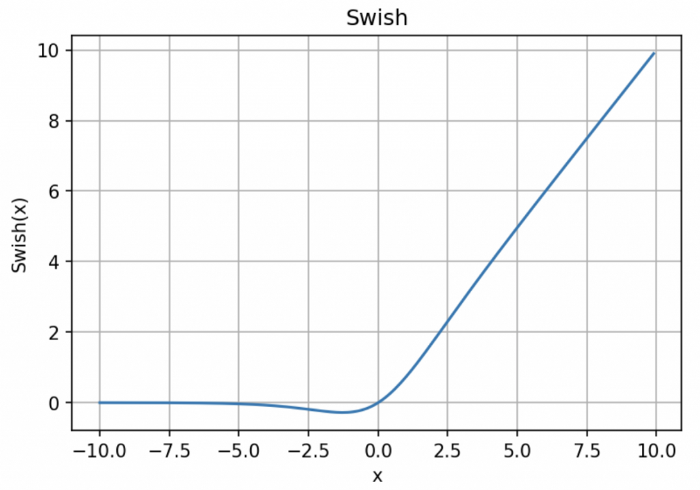
- Swish 的设计受到了 LSTM 和高速网络中 gating 的 sigmoid 函数使用的启发。我们使用相同的 gating 值来简化 gating 机制,这称为 self-gating。
- self-gating 的优点在于它只需要简单的标量输入,而普通的 gating 则需要多个标量输入。这使得诸如 Swish 之类的 self-gated 激活函数能够轻松替换以单个标量为输入的激活函数(例如 ReLU),而无需更改隐藏容量或参数数量。
主要优点:
- 【无界性】有助于防止慢速训练期间,梯度逐渐接近 0 并导致饱和。
- 平滑度在优化和泛化中起了重要作用。
并非有界性就是不好的。有界性的优势在于其激活函数可以具有很强的正则化,并且可以解决较大的负输入问题。
10. Maxout
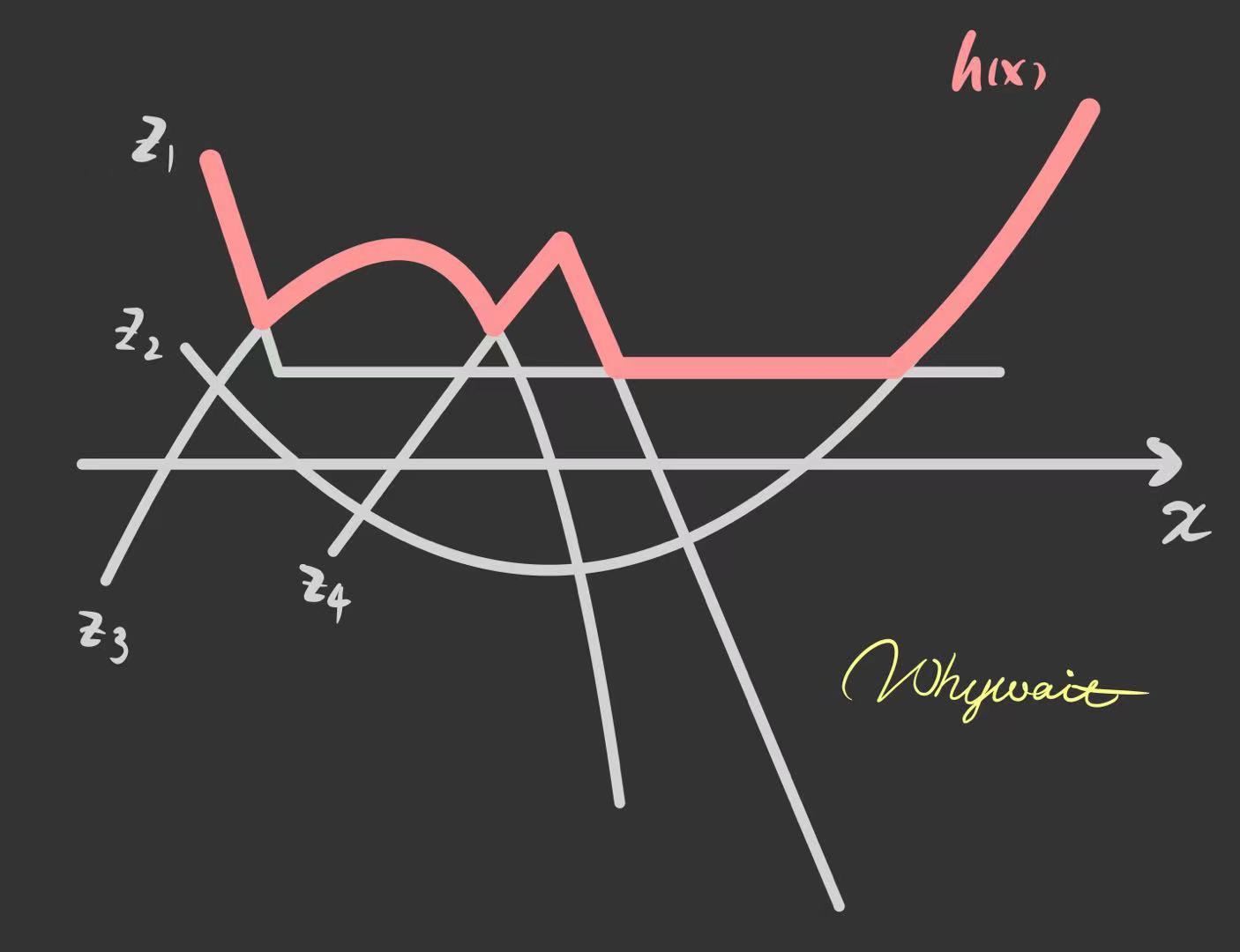
- 在 Maxout 层,激活函数是输入的最大值,因此只有 2 个 maxout 节点的多层感知机就可以拟合任意的凸函数。
- 单个 Maxout 节点可以解释为对一个实值函数进行分段线性近似 (PWL) ,其中函数图上任意两点之间的线段位于图(凸函数)的上方。
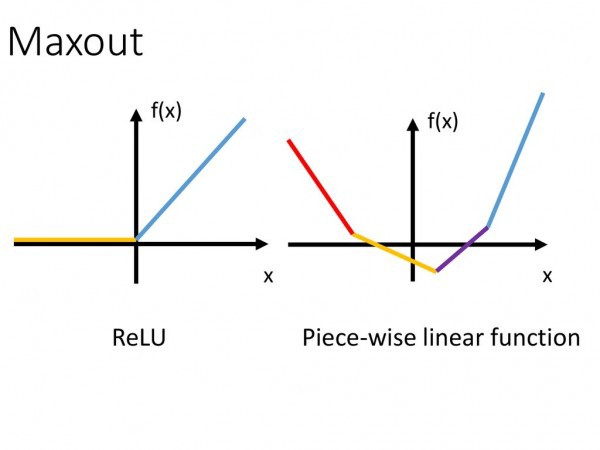
- 同样也可以用在 d 维向量实现:
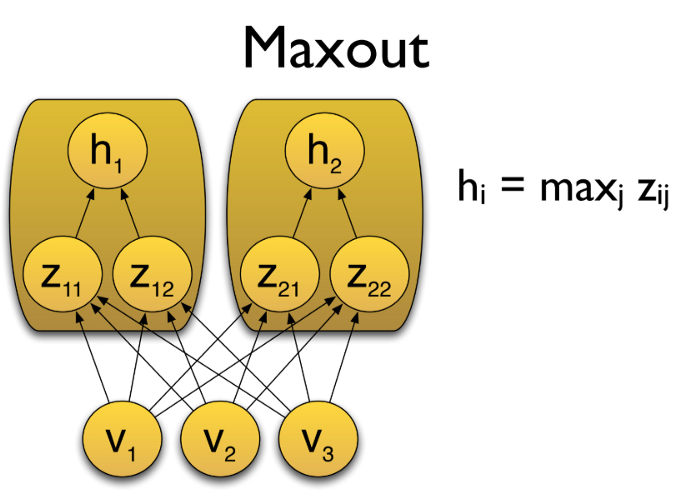
小证明
每一个Maxout节点都相当于一个凸函数的近似,对于一个连续的PWL函数$g(x)$而言,其肯定可以被两个凸函数$h_1(x), h_2(x)$ 表示:
\[g(x)=h_1(x)-h_2(x)\]这也是 由两个 Maxout 节点组成的 Maxout层可以很好近似任何连续函数的原因。
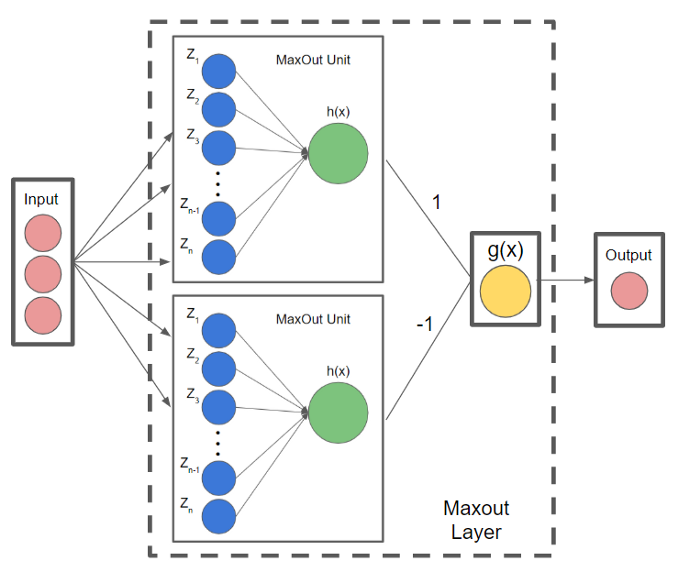
从上图中可以看出,$z_i$ 相当于许多不同的函数,而$h(x)$相当于这些函数中的最大值,如下图。