Non-Maximum Suppression (NMS)
NMS
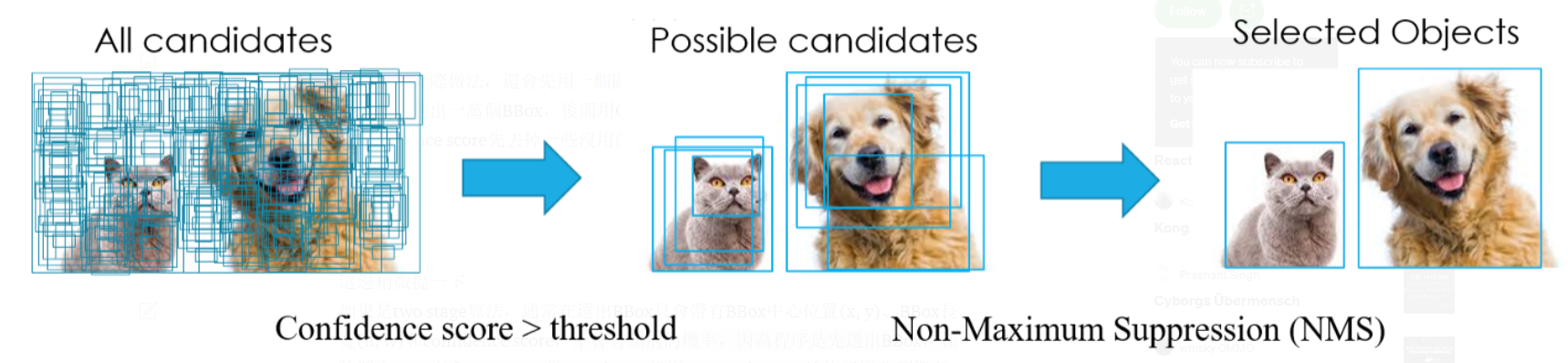
Input and Output
Input: A list of Proposal boxes $B$, corresponding confidence scores $S$ and overlap threshold $N$.
Output: A list of filtered proposals $D$.
Algorithm
- Select the proposal with highest confidence score, remove it from $B$ and add it to the final proposal list $D$. (Initially $D$ is empty).
- Now compare this proposal with all the proposals — calculate the IOU (Intersection over Union) of this proposal with every other proposal. If the IOU is greater than the threshold $N$, remove that proposal from $B$.
- Again take the proposal with the highest confidence from the remaining proposals in $B$ and remove it from $B$ and add it to $D$.
- Once again calculate the IOU of this proposal with all the proposals in $B$ and eliminate the boxes which have high IOU than threshold.
- This process is repeated until there are no more proposals left in $B$.
Graphical Representation
Differences using different threshold $N$
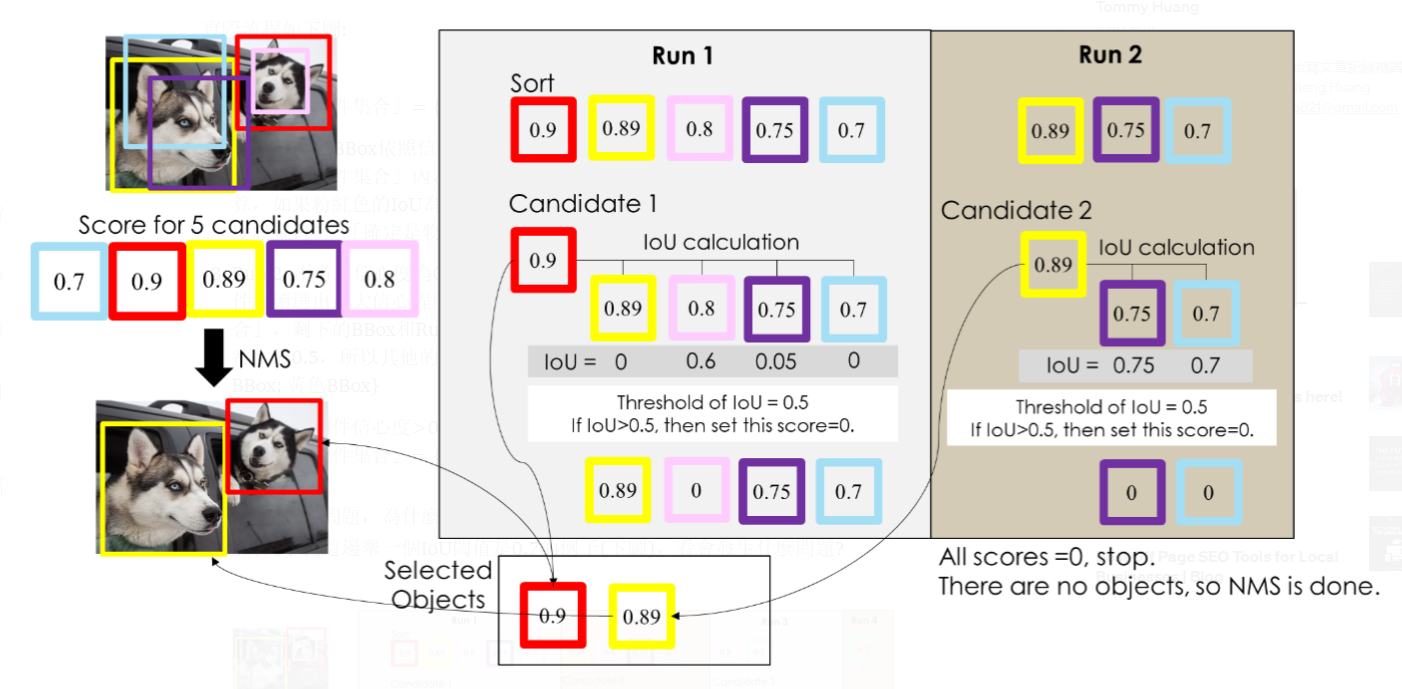
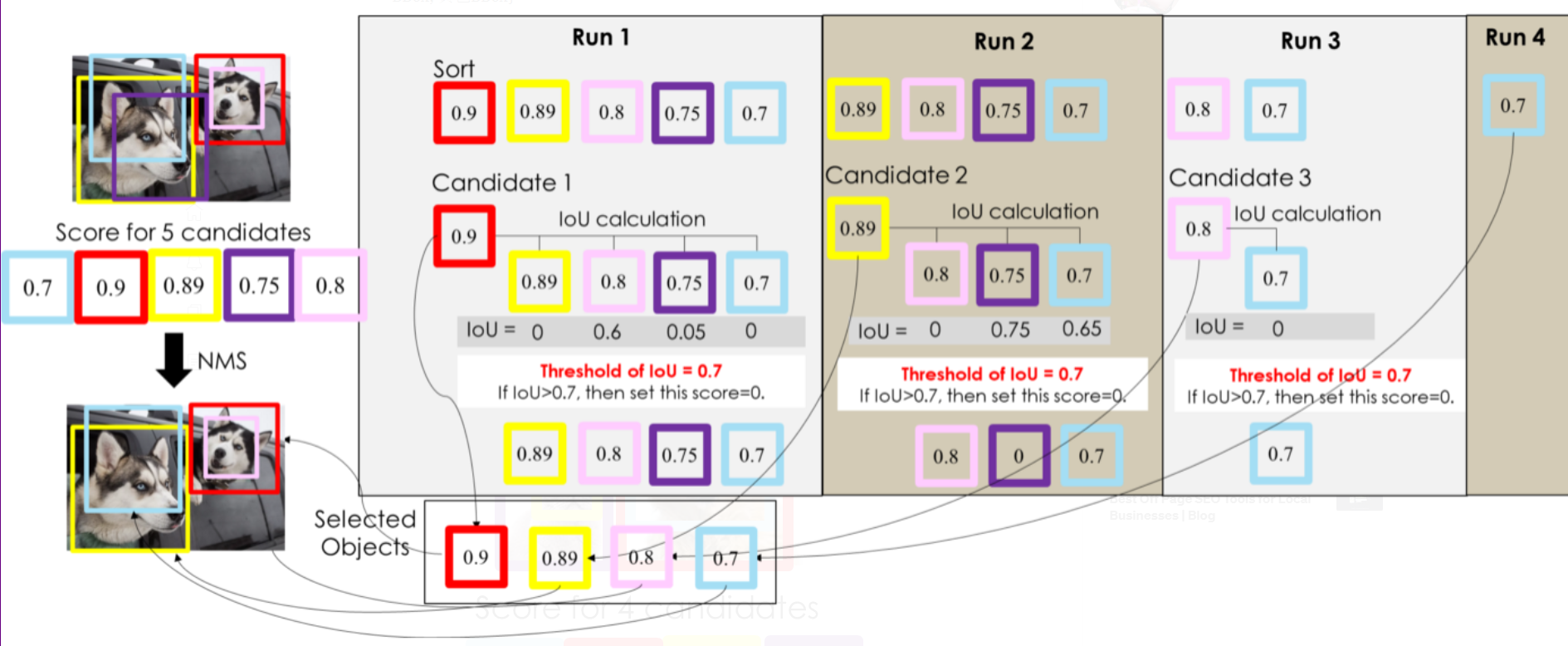
Hence, threshold $N=0.5$ is better than $N=0.7$, which means if the threshold $N$ of IOU is set too large, the objectives will be detected repeatedly.