子空间分析与跟踪(1) —— 子空间的一般理论
1. 子空间的基

张成子空间$W$的每个向量称为$W$的生成元(generator),而所有生成元组成的集合${u_1,…,u_m}$称为子空间的张成集(spanning set)。
一个只包含了零向量的向量子空间称为平凡子空间(trivial subspace)。非平凡子空间可以包含零向量而非不包含零向量。
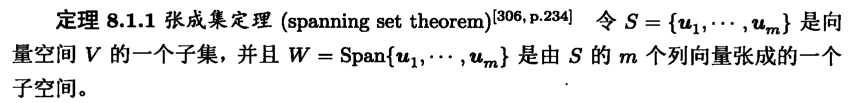
关于子空间的基:1)当使用张成集定理从向量集合$S$中删去某个向量时,一旦$S$变成线性无关向量的集合,则必须立即停止从$S$内再删除向量。2)一组基也是线性无关向量尽可能大的集合。
当提及某个向量子空间的基时,并非说它是唯一的基,而只是强调它只是其中的一组基。 (所有的基必然含有相同数目的线性无关向量。)

2. 无交连、正交与正交补
【子空间的交】子空间$S_1,S_2,…,S_n$共同拥有的所有向量组成的集合。符号表示为:$S=S_1\cap S_2\cap …\cap S_n$
【无交连(disjoint)】$S=S_1\cap S_2\cap …\cap S_n={\mathbf{0}}$
【子空间的直和】无交连的子空间的并 $S=S_1\cup S_2\cup …\cup S_n$,记作:$S=S_1\oplus S_2\oplus …\oplus S_n$
【正交子空间】子空间$S_1,S_2,…,S_n$为正交子空间,记作$S_i\perp S_j, i\ne j$,若$a_i\perp a_j$对所有$a_i\in S_i,a_j\in S_j(i\ne j)$ 恒成立。
若一向量与子空间$S$的所有向量都正交,则称该向量正交于子空间$S$。
【正交补(orthogonal complement)】与子空间$S$正交的所有向量的集合组成的一个向量子空间,记作$S^\perp$
\[\dim(S)+\dim(S^\perp)=\dim(V)\]
无交连子空间、正交子空间和正交补空间的关系:
- 无交连是比正交更弱的条件。两个子空间无交连,只是表明这两个子空间没有任何一对非零的共同向量,并不意味着这两个向量之间的任何其他关系。与之相反,当子空间$S_1$和$S_2$正交时,任意两个向量$x\in S_1$和$y\in S_1$都是正交的,它们之间没有任何相关的部分,即$S_1$和$S_2$一定是无交连的。
- 正交补空间是一个比正交子空间更严格的概念。$S$的正交补一定与$S$正交,但与$S$正交的子空间一般不是$S$的正交补。
【向量的正交分解】向量空间$\mathcal{R}^m$的每一个向量$u$都可以用唯一的方式分解为子空间$S$的向量$x$与正交补$S^perp$的向量$y$之和,即 $u=x+y,x\perp y$,这一分解形式称为向量的正交分解。
一个特征向量定义一个一维子空间,它相对于左乘矩阵$A$是不变的。
【不变子空间】一个子空间$S\subseteq\mathcal{C}^n$称为(相对于)$A$不变的,若
\[x\in S~~~\Rightarrow~~~Ax\in S\]
- 实对称矩阵不同的特征值对应的特征向量是相互正交的;
- 正交矩阵属于不同特征值的特征向量一定正交。
由$A$的特征向量张成的子空间$S$是相对于$A$不变的子空间。
零空间 $Null(A-\lambda I)$ 称为矩阵$A$与特征值$\lambda$对应的特征空间。
【零空间】零空间是在线性映射(即矩阵)的背景下出现的。在数学中,一个算子 A 的零空间是方程 Av = 0 的所有解 v 的集合。它也叫做 A 的核,核空间。如果算子是在向量空间上的线性算子,零空间就是线性子空间。因此零空间是向量空间。$^{[2]}$
【矩阵的特征对】$(特征值\lambda, 特征向量u)$
$\lambda(B)$:矩阵$B$所有特征值组成的集合。
3. 子空间的正交投影与夹角
【投影算子】一线性矩阵变换$P$,讲$\mathcal{R}^n$的向量$x$映射为子空间$S$的向量$x_1$。这样一种线性变换称为沿着$H$方向到$S$的投影算子(projector onto S along H),常用符号$P_{S\vert H}$。
【正交投影】若子空间$H$是$S$的正交补,则$P_{S\vert S^\perp}x$是将$\mathcal{R}^n$的向量$x$沿着与子空间$S$垂直的方向,到子空间$S$的投影,故称$P_{S\vert S^\perp}x$为到子空间$S$的正交投影,常用$P_S$作数学符号。

后面两个条件,一个要求正交投影算子必须是幂等算子,一个要求正交投影算子必须具有复共轭对称性即Hermitian性。
$Range(P)$ 表示矩阵$P$的列空间。$^{[3]}$
根据正交投影算子的定义知,若$x\in\mathcal{R}^n$,则有$Px\in S$和$(I-P)x\in S^\perp$
【正交投影算子的唯一性】到一个子空间的正交投影算子是唯一确定的。
令 $n\times r$矩阵$W$具有满列秩,其列空间$H=Col(W)$,并令$x$为$\mathcal{C}^n$空间的一任意向量,则 $x$ 到 $H$ 子空间的投影为
\[P_Hx=W(W^HW)^{-1}W^Hx\]通过验证可以发现 $P_H=W(W^HW)^{-1}W^H$ 满足定义8.1.5中的三个条件,故而可知 $P_H$为正交投影因子。
【斜投影算子】如果子空间$H$与$S$不正交,则$P_{S\vert H}x$称为向量$x$沿着子空间$H$的方向,到子空间$S$的斜投影,并称$P_{S\vert H}x$为斜投影算子。


图示说明如下

【F范数】Frobenius norm(Frobenius 范数),有不同的定义方式$^{[4]}$。更多定义为:矩阵A的Frobenius范数定义为矩阵A各项元素的绝对值平方的总和开根。 $^{[5]}$
4. 主角与补角
Hilbert空间即完备的内积空间,也就是一个带有内积的完备向量空间。$^{[6]}$

【最小角度】所有主角中最小的主角。


如果两个子空间无交连,则这两个子空间之间的补角与最小角度相同,即$\varPhi_C(H_1,H_2)=\varPhi(H_1,H_2)$
5. 子空间的旋转
【正交强迫一致问题】

从子空间的角度看问题,正交强迫一致的运算相当于使列空间$Col(B)$旋转进入列空间$Col(A)$内。
为了实现$\Vert A-BQ\Vert^2_F$最小化,应该选择正交矩阵$Q$使得$BQ$具有与$A$完全相同的非对角元素,并且对角元素的平方和尽可能接近。如此一来,可以将其写成迹函数的形式
\[\Vert A-BQ\Vert^2_F=tr(A^TA)+tr(B^TB)-2tr(Q^TB^TA)\]然后找出$tr(Q^TB^TA)$上界。通过矩阵乘积$B^TA$的奇异值分解得到$B^TA=U\Sigma V^T$,再定义正交矩阵$Z=V^TQ^TU$,则有
\[tr(Q^TB^TA)=tr(Q^TU\Sigma V^T)=tr(V^TQ^TU\Sigma)=tr(Z\Sigma)=\sum_{i=1}^{n}z_{ii}\sigma_i\le\sum_{i=1}^{n}\sigma_i\]using $tr(AB)=tr(BA)$
当且仅当$Z=I$即$Q=UV^T$时,等号成立。即得结论,若$B^TA=U\Sigma V^T$是矩阵乘积$B^TA$的奇异值分解,选择$Q=UV^T$,则$tr(Q^TB^TA)$取最大值,从而使$\Vert A-BQ\Vert^2_F$取最小值。
解矩阵$Q$称为矩阵乘积$B^TA$的正交极因子(orthogonal polar factor),因为正交强迫一致问题相当于将矩阵$A$分解为$BQ$,而这种矩阵分解称为极式分解(polar decomposition)。
[1] 张贤达. 矩阵分析与应用[M]. 清华大学出版社有限公司, 2004.
[2] Farjoun E D. Cellular spaces, null spaces and homotopy localization[M]. Springer, 2006.
[4] 矩阵范数
[5] Frobenius norm(Frobenius 范数)s
[6] 希尔伯特空间