子空间分析与跟踪（2） —— 列空间、行空间与零空间

Published: February 11, 2022 by Authur Lee

Categories:
Math 7

矩阵的列空间、行空间与零空间
- 矩阵零空间与列空间之间的对比
子空间的基构造
- 初等变换法
- QR分解
基本空间的标准正交基构造
构造两个零空间交的标准正交基

矩阵的列空间、行空间与零空间

列空间（column space）或列张成（column span）。复矩阵$A$列向量的所有线性组合的集合构成的一个子空间，用符号 $Col(\mathbf{A})$ 表示。
行空间（row space）或行张成（row space）。复矩阵$A$的复共轭行向量的所有线性组合的集合构成的一个子空间，用符号 $Row(\mathbf{A})$ 表示。

在数学中，复共轭是一对称为复数的两分量数。这些复数中的每一个都具有添加到虚数部分的实数部分。尽管它们的值相等，但是这对复共轭数中的虚部之一的符号与另一个的符号相反。尽管具有虚构的分量，但复杂的共轭物仍用于描述物理现实。尽管存在虚部，复共轭的使用仍然有效，因为当两个分量相乘时，结果是实数。$^{[2]}$

\[\begin{aligned} Col(\mathbf{A})&=Span(\mathbf{A})\\ Row(\mathbf{A})&=Col(\mathbf{A}^H)=Span(\mathbf{A}^H) \end{aligned}\]

复矩阵 $\mathbf{A}$ 的行空间与复共轭转置矩阵 $\mathbf{A}^H$ 的列空间等价。复共轭转置矩阵为$A_H=(\bar{A})^T$。$^{[3]}$

值域（range）。设$A$是一个$m\times n$复矩阵，则$A$的值域定义为

\[Range(A)=\{y\in\mathcal{C}^m\vert Ax=y,x\in\mathcal{C}^n\}\]

零空间（null space）。也称为核（kernel）。对于$A_{m\times n}$，零空间定义为

\[Null(A)=Ker(A)=\{x\in\mathcal{C}^m\vert Ax=0\}\]

零空间的维数称为$A$的零化维（nullity）

\[nullity(A)=dim[Null(A)]\]

矩阵$A$的值域就是$A$的列空间。

\[Range(A)=Col(A)\]

秩（rank）

\[rank(A)=dim[Col(A)]=dim[Range(A)]\]

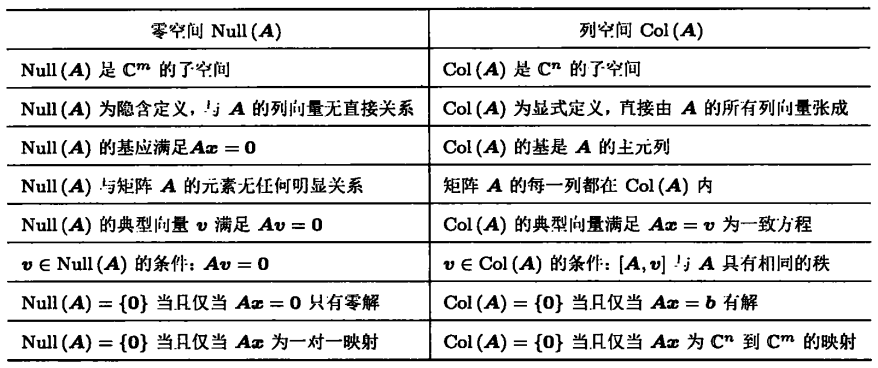
矩阵零空间与列空间之间的对比

子空间的基构造

初等变换法

由于初等行变换与初等列变换得到的行空间与列空间的基向量等价，故选择任一种初等变换均可。习惯上使用初等行变换。不过，若矩阵的列数明显少于行数时，初等列变换需要较少的次数。

矩阵 $A_{m\times n}$的列（行）空间与零空间维数之间的关系：

\[rank(A)+dim[Null(A)]=n\]

QR分解

QR分解法是三种将矩阵分解的方式之一。其将矩阵分解成一个正交矩阵与一个上三角矩阵的积。QR分解经常用来解线性最小二乘法问题。$^{[4]}$

基本空间的标准正交基构造

初等变换法 + Gram-Schmidt正交化

初等变换法得到线性无关的基向量，对于线性无关的基向量，可以使用Gram-Schmidt正交化达到在基本空间中构造标准正交基的目的。

Gram-Schmidt正交化的基本想法，是利用投影原理在已有正交基的基础上构造一个新的正交基。$^{[5]}$

奇异值分解法

相较于初等变换法和Gram-Schmidt正交化的组合套餐而言，奇异值分解法更方便。

$rank(A)=r$的矩阵$A_{m\times n}$具有如下奇异值分解：

\[A=U\Sigma V^H\]

其中，

\[\begin{matrix} U=&[U_r,\tilde{U}_r],&V=[U_r,\tilde{V}_r], \end{matrix}\\ \Sigma=\begin{bmatrix} \Sigma_r & O_{r\times (n-r)}\\ O_{(m-r)\times (n-r)} & O_{(n-r)\times (n-r)} \end{bmatrix}\]

$U_r$: $m\times r$
$\tilde{U}_r$: $m\times (m-r)$
$V_r$: $n\times r$
$\tilde{V}_r$: $n\times (n-r)$
$\Sigma=diag(\sigma_1,\sigma_2,…,\sigma_r)$