子空间分析与跟踪(4) —— Grassmann流形和Stiefel流形
本文考虑的是目标函数 $J(W)$ 的最小化问题。其中 $W$ 为 ${n\times r}$ 矩阵。
两类常用的约束
两类对矩阵 $W_{n\times r}$ 常用的约束:
【1】正交约束(orthogonality constraint)
\[\begin{matrix} W^HW=I_r(n\ge r)&or&WW^H=I_n(n<r) \end{matrix}\]【2】齐次性约束(homogeneity constraint)
\[J(W)=J(WQ),Q_{r\times r},Q^HQ=I\]一些说明
- 如果矩阵 $W_{n\times r}$ 满足正交约束,该矩阵 $W_{n\times r}$ 被称为半正交矩阵;
- $Q_{r\times r},Q^HQ=I$表示 $Q$ 是一个 $r\times r$ 的正交矩阵;
- 齐次,指的是所列的式子只和 $x^n,y^n$ 相关,不存在 $x^m,y^l(m\ne n, l\ne n)$ 的项,包括常数项也只有 $0$。$^{[4]}$
正交矩阵和半正交矩阵的区别$^{[2]}$
半正交矩阵要满足的条件:
\[实矩阵,且 MM^T=I\]正交矩阵要满足的条件:
\[实方阵,且 AA^T=I\]不变子空间
【线性流形】令 $H$ 是 $V$ 空间的子空间,由 $H$ 张成的线性流形 $\mathcal{L}$
\[\mathcal{L}=\left\{\xi:\xi=\sum_{i=1}^na_i\eta_i,\eta_i\in H\right\}\]【等价矩阵】矩阵列向量张成的子空间相同。
【不变子空间】等价的矩阵集合具有相同的列空间,即子空间相对于基的任意选择是不变的。此意义上说,这类子空间也称为不变子空间。
【等价子空间类】由所有相同的子空间组成。
【证明】等价子空间
核心思想:任意向量到该两子空间的投影相同,则该两子空间为等价子空间。
投影矩阵和正交投影矩阵的表示
到子(列)空间的投影矩阵 $P_H$
\[P_H=W(W^HW)^{-1}W^H\]到子(行)空间的投影矩阵 $P_H$
\[P_H=W^H(WW^H)^{-1}W\]正交投影矩阵
\[P_H^\perp=I-P_H\]证明过程

或者称 $n\times r$ 满列秩矩阵 $W$ 的列空间 $Col(W)$ 是相对于 $r\times r$ 非奇异矩阵 $M$ 不变的子空间。
Grassmann流形
同时使用正交约束和齐次性约束。
因为正交约束,我们有 $W^HW=I$ (列空间) 或者 $WW^H=I(行空间)$,所以
- 不变的列空间 $Col(W)$ 可等价描述为矩阵乘积 $WW^H$ 不变;
- 不变的行空间 $Row(W)$ 可等价描述为矩阵乘积 $W^HW$ 不变。
【一些说明】在上面“【证明】等价子空间”中,我们可知任意向量到两个子空间的投影相同,那么这两个子空间就是不变子空间。如此,若两个子空间为不变子空间,那么它们的投影矩阵 $P_{H_1}$ 以及 $P_{H_2}$ 相同,而因为正交约束的存在,可得上面两点。(行空间和列空间的情况不一样,但是中间相差一个$^H$,即 $行空间=列空间^H$ 而来。
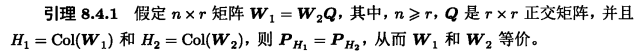
- 若一个矩阵等于另外一个矩阵右乘一个正交矩阵,那么这两个矩阵等价或者张成相同的列空间。
特别地,若 $W_{n\times r}$ 满足正交约束条件以及齐次性约束条件,那么极小化问题的解不是一个 $W$ 矩阵,而是由 $WQ$ 组成的矩阵集合。
矩阵集合内的任何一个矩阵的列向量都张成相同的$\mathbb{C}^r$子空间。
$\mathbb{C}^n$内的这一子空间集合称为 Grassmann 流形,记为
\[Gr(n,r)=\{W\in\mathbb{C}^{n\times r}:W^HW=I_r,WW^H=同一矩阵\}\]Grassmann流形小结
极小化问题
\[\min J(W)\]约束条件为
\[\begin{matrix} subject~to:& W^HW=I_r,&J(W)=J(WQ),&Q^HQ=QQ^H=I_r \end{matrix}\]解不是单个矩阵,而是称为 Grassmann 流形的矩阵集合。即Grassmann 流形的任何一个点都是同时具有正交约束和齐次性约束的极小化问题的解。
Stiefel流形
\[\begin{matrix} \min J(W)&subject~to&W^HW=I_r \end{matrix}\]只使用正交约束。
此最优化问题的解为 $n\times r$ 半正交矩阵的集合。
【Stiefel流形】所有 $n\times r$ 半正交矩阵的集合称为 Stiefel 流形,记为
\[Str(n,r)=\{W\in\mathbb{C}^{n\times r}:W^HW=I_r\}\]联系与区别
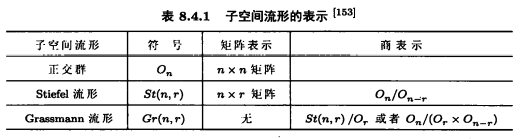
Grassmann流形 VS Stiefel流形

Grassmann流形,Stiefel流形,and 正交群
正交群的概念

三者之间的关系
\[\begin{aligned} St(n,r)&=O_n/O_{n-r}\\ Gr(n,r)&=St(n,r)/O_r\\ Gr(n,r)&=O_n/(O_r\times O_{n-r}) \end{aligned}\]详细说明见文末附录
小结
矩阵 Rayleigh 商
矩阵Rayleigh商 以及 推广的(标量)Rayleigh商

Rayleigh商
\[\frac{x^HAx}{x^Hx}\]矩阵Rayleigh商与Rayleigh的定义中通常约定$x^Hx=1$类似,矩阵Rayleigh商假设$X^HX=I$($X$是Stiefel流形上的点)。矩阵Rayleigh商利用了Stiefel流形定义。
性质

Stiefel流形、Grassmann流形与Rayleigh商之间的关系
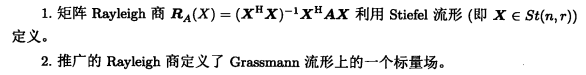
【标量场】标量场是指一个仅用其大小就可以完整表征的场。一个标量场u 可以用一个标量函数u(x,y,z)来表示。标量场分为实标量场和复标量场,其中实标量场是最简单的场,它只有一个实标量,而复标量是一个复数的场,它有两个独立的场量,这相当于场量有两个分量。最常用的标量场有温度场,电势场,密度场,浓度场等等。在标量场中,需要注意的是等值面、方向导数、梯度这几个量。$^{[3]}$
参考
[1] 张贤达. (2004). 矩阵分析与应用. 清华大学出版社有限公司.
[2] Leon晋. (2021, May 25). 半正交矩阵的含义是什么? Retrieved February 15, 2022, from 知乎: https://www.zhihu.com/question/461150139/answer/1903508845
[3] 标量场, from 百度百科: https://baike.baidu.com/item/%E6%A0%87%E9%87%8F%E5%9C%BA/9811898
[4] lyounger. (2014, December 5). 齐次性到底描述了什么? Retrieved February 15, 2022, from 知乎: https://www.zhihu.com/question/25552461
附录
