子空间分析与跟踪(5) —— 投影逼近子空间跟踪
先知道
快速算法需要满足的性质
特征子空间的跟踪与更新主要用于实时信号处理。
对于实时信号处理而言,我们的算法需要满足快速的要求。而对于一个快速算法而言,我们需要考虑到以下因素
- $n$ 时刻的子空间可以通过更新 $n-1$ 时刻的子空间获得;
- $n-1$ 时刻到 $n$ 时刻的协方差矩阵的变化应该尽可能是低秩变化(最好是秩1变化或者秩2变化);
- 只需要跟踪低维子空间。
特征子空间跟踪与更新方法分类
主要分为以下四类:
- 正交基跟踪。只使用噪声子空间特征向量的正交基,而无需使用特征向量本身。
- 秩1更新。将非平稳信号在k时刻的协方差矩阵看作是k-1时刻的协方差矩阵与另外一个秩等于1的矩阵(秩等于1的矩阵为观测向量的共轭转置与其本身的乘积,即 $x^Hx$)之和。协方差矩阵的特征值分解的跟踪与所谓的秩1更新密切相关。
- 投影逼近。将特征子空间的确定当作一个无约束最优化问题来求解。相应的方法称为投影逼近子空间跟踪。也是本文主要介绍的内容。
- Lanczos子空间跟踪。利用Lanczos型迭代和随即逼近的概念,可以进行时变数据矩阵的子空间跟踪。
投影逼近子空间跟踪的基本理论
【证明】具有正交性约束和齐次性约束的极小化问题 $\min J(W)$ 可以等价为一个无约束的最优化问题
将目标函数转化为迹函数


综上,对于极小化问题 $J(W)$ 而言,
- 存在 $J(W)$ 的全局极小点 $W$;
- 不存在 $J(W)$ 的局部极小点。
- 同时也可以知道极小点 $W$ 与自相关矩阵 $C$ 的信号子空间之间的关系。
平稳点和鞍点的区别见文末附录

目标函数 $J(W)$ 转变为分解问题
两种方法:奇异值分解或者特征值分解问题。

奇异值分解和特征值分解的异同见文末附录。
在实际应用中,自相关矩阵 $C$ 随时间变化,其特征值和特征向量也随时间变化。在时变的情况下,我们将目标函数写为 $J(W(t))$ 即可。
投影逼近子空间跟踪算法
PAST

PAST 算法从数据向量中提取信号子空间,是一种主分量分析方法。
“数据向量中提取信号子空间”:
PASTd
若r=1,则由PAST算法可得PASTd算法。

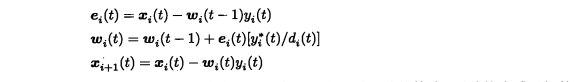
OPAST

附录
平稳点(驻点)和鞍点的区别
- 平稳点(驻点):导数为零
- 鞍点:不是局部极值点的驻点。
奇异值和特征值的异同$^{[2]}$
奇异值与特征值都被用于描述矩阵作用于某些向量的标量,都是描述向量模长变化幅度的数值。它们的差异在于:
- 特征向量描述的是矩阵的方向不变作用(invariant action)的向量;
- 奇异向量描述的是矩阵最大作用(maximum action)的方向向量。
参考
[1] 张贤达. (2004). 矩阵分析与应用. 清华大学出版社有限公司.
[2] gwave. (2021, April 26). 奇异值与特征值辨析 Retrieved February 15, 2022, from 知乎: https://zhuanlan.zhihu.com/p/353637184