知识蒸馏
知识蒸馏是一种教师-学生(Teacher-Student)训练结构,通常是已训练好的教师模型提供知识,学生模型通过蒸馏训练来获取教师的知识。以轻微的性能损失为代价将复杂教师模型的知识迁移到简单的学生模型中。
模型压缩与模型增强
教师模型都是提前训练好的复杂网络,模型压缩和模型增强都是将教师模型的知识迁移到学生模型中。
- 模型压缩:教师网络在相同的带标签的数据集上指导学生网络的训练来获得简单而高效的网络模型。
- 模型增强:强调利用其他资源(如无标签或者跨模态的数据)或知识蒸馏的优化策略(如互相学习和自学习)来提高一个复杂学生模型的性能。
知识蒸馏和迁移学习的异同
知识蒸馏和迁移学习都涉及到知识的迁移,但是主要有四点不同:
- 数据域不同。知识蒸馏中的知识通常是在同一个目标数据集上进行迁移,而迁移学习中的知识往往是不同目标的数据集上进行转移。
- 网络结构不同。知识蒸馏的两个网络可以是同构或者异构的,而迁移学习通常是在单个网络上利用其他领域的数据知识。
- 学习方式不同。迁移学习使用其它领域的丰富数据的权重来帮助目标数据的学习,而知识蒸馏不会直接使用学到的权重。
- 目的不同。知识蒸馏通常是训练一个轻量级的网络来逼近复杂网络的性能,而迁移学习是将已经学习到相关任务的权重来解决目标数据集的样本不足问题。
小结:知识蒸馏更强调的是知识的迁移,而非权重的迁移。
逻辑单元与类概率
逻辑单元是Softmax激活的前一层,而类概率由Softmax激活函数转化而来:
\[p_i(z_i)=\frac{\exp(z_i)}{\sum_{j=1}^k\exp(z_j)}\]其中,$z_i$是第$i$类的逻辑单元值,$p_i$是第$i$类的类概率,$k$表示类别的数量。网络输出逻辑单元和类概率的关系如下图所示。
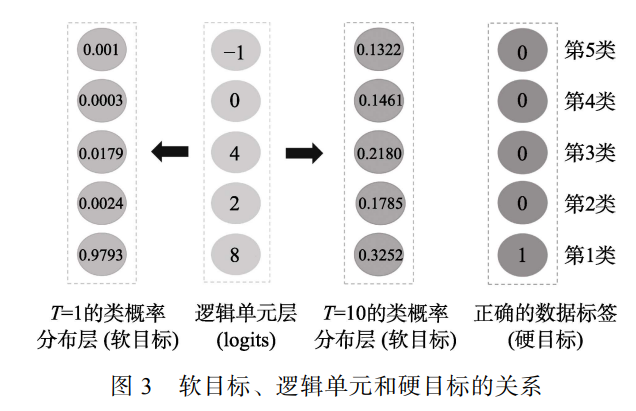
在与知识蒸馏相近的早期工作中,大多都涉及小网络利用大网络的输出知识,且在训练和测试阶段使用的知识都是一致的,要么使用逻辑单元,要么使用类概率。于是会面临以下问题:
- 如果使用逻辑单元表示知识,这些不受约束的值在测试的时候可能会包含噪声信息。
- 如果使用类概率表示知识,因为负标签的概率被Softmax压扁后将会接近零,导致在网络训练时负标签蕴含的信息丢失。
为解决上述问题,软目标的概念(带有参数$T$的类概率)于2015年被引入并提出了知识蒸馏的概念。软目标的计算公式的如下:
\[p_i(z_i,T)=\frac{\exp(z_i/T)}{\sum_{j=0}^k\exp(z_i/T)}\]其中,$T$为温度系数,用来控制输出概率的软化程度。$T=1$时,软目标即表示网络输出softmax的类概率;而当$T\to\infty$时,此时表示网络输出逻辑单元。(在参考论文2中被证明)
逻辑单元实际上是知识蒸馏的一个特例。
通常,知识蒸馏在测试时令$T=1$,在训练的时候则使用较大的$T$值。测试时$T=1$,不同逻辑单元值的软目标的差异很大,所以在测试时能够较好地区分正确和错误的类;在训练时,较大的$T$值的软目标差异比$T=1$时的差异小,模型训练时会对较小的逻辑单元给予更多的关注,从而使学生模型学习到这些负样本和正样本之间的关系信息。
这样的隐藏在教师模型中的关系信息称为“暗知识”(Dark Knowledge),而知识蒸馏就是在训练的过程中将教师模型的暗知识传递到学生模型中。
除了利用教师模型输出的软目标之外,Hinton等人还发现在在训练过程中加上正确的数据标签(即硬目标)会使学习效果更好。具体操作方法是对两个不同的目标函数进行权重平均。第一个目标函数是具有较高值$T$值教师模型和具有较高$T$值学生模型的交叉熵损失(称为蒸馏损失);第二个目标函数是$T=1$的学生和硬目标的交叉熵损失(称为学生损失)。因此,知识蒸馏的总损失可以表示为:
\[L_{total}=\lambda\cdot L_{KD}(p(u,T),p(z,T))+(1-\lambda)\cdot L_S(y,p(z,1))\]其中,$\lambda$为超参数,$L_S$为学生损失。$\lambda$通常为经验调参的固定值,也可以动态的调整。学生损失表示为
\[L_S(y,p(z,1))=-\sum_{i=1}^ky_i\log(p_i(z,1))\]其中$y$是硬标签的向量。知识蒸馏的框架如下图所示。
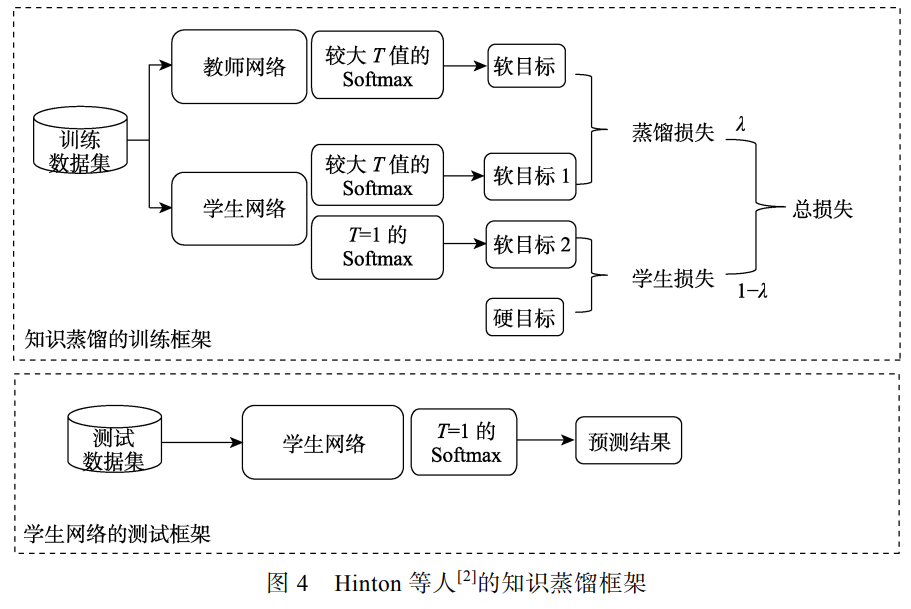
知识蒸馏的作用机制
- 软目标为学生模型提供正则化约束。软目标通过提供标签平滑和置信度惩罚对学生模型施加正则化训练。因此,即使没有强大的教师模型,学生模型仍然可以通过自己训练或手动设计的正则化项得到增强。
- 软目标为学生项目提供了“特权信息”(Privileged Information)。教师模型在训练过程中将软目标的 暗知识 迁移到学生模型中,而学生模型在测试过程中并不能直接使用暗知识,从该角度理解,知识蒸馏通过软目标来为学生模型传递“特权信息”。
- 软目标引导了学生模型优化的方向。
蒸馏的知识形式
知识蒸馏的首要问题是要明确迁移教师网络中的哪些知识。
从学生解题的角度,四种知识形式可以形象比喻为:
- 输出特征知识提供了解题的答案;
- 中间特征值是提供了解题的过程;
- 关系特征知识提供了解题的方法;
- 结构特征知识提供了完整的知识体系。
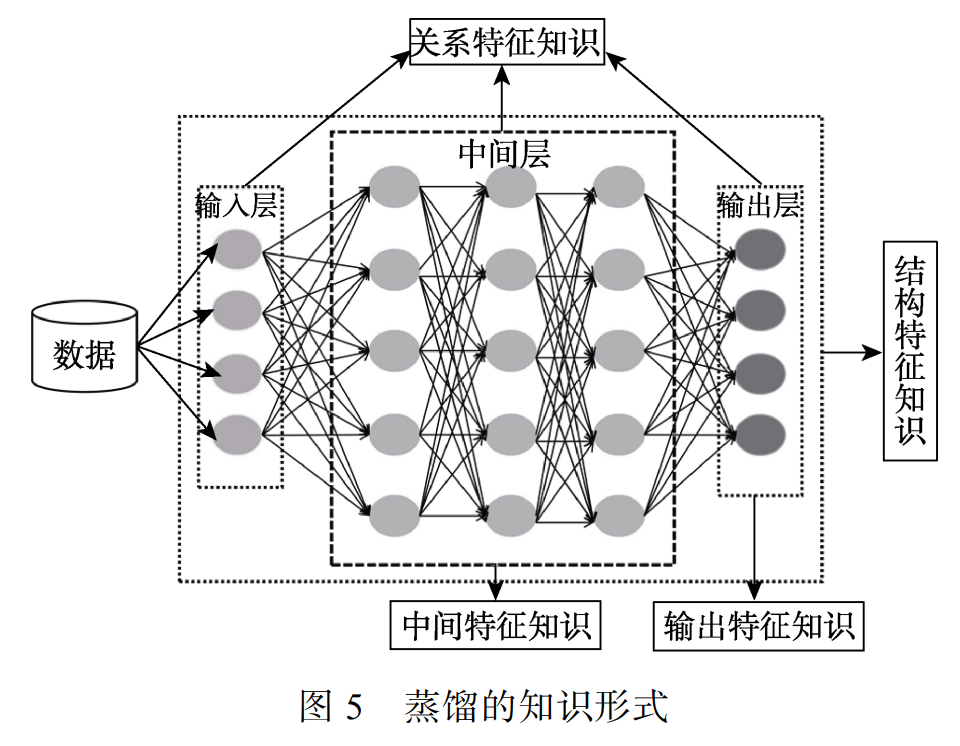
输出特征知识
- 输出特征知识通常指教师模型的最后一层特征,主要包括逻辑单元和软目标的知识。
- 输出特征知识蒸馏的主要思想是促进学生能够学习到教师模型的最终预测,以达到和教师模型一样的预测性能。
- 不同任务教师模型的最后一层输出特征是不一样的。
中间特征知识
中间特征的知识蒸馏。主要思想是从教师中间的网络层中提取特征来充当学生模型中间层输出的提示(Hint)。在使用教师模型输出特征知识的同时,还要使用教师模型隐含层中的特征图知识。
学生模型学习教师模型中间隐含层的损失为:
\[L_{Hint}(W_{Guided},W_r)=\frac{1}{2}\Vert u_h(x;W_{Hint})-r(u_g(x;W_{Guided});W_r)\Vert^2\]$W_{Hint}$以及$W_{Guided}$分别为教师前$h$层的权重以及学生前$g$层的权重;$u$为特征的输出。$r$为针对师生间的隐含层尺寸不一致而设计的回归函数。
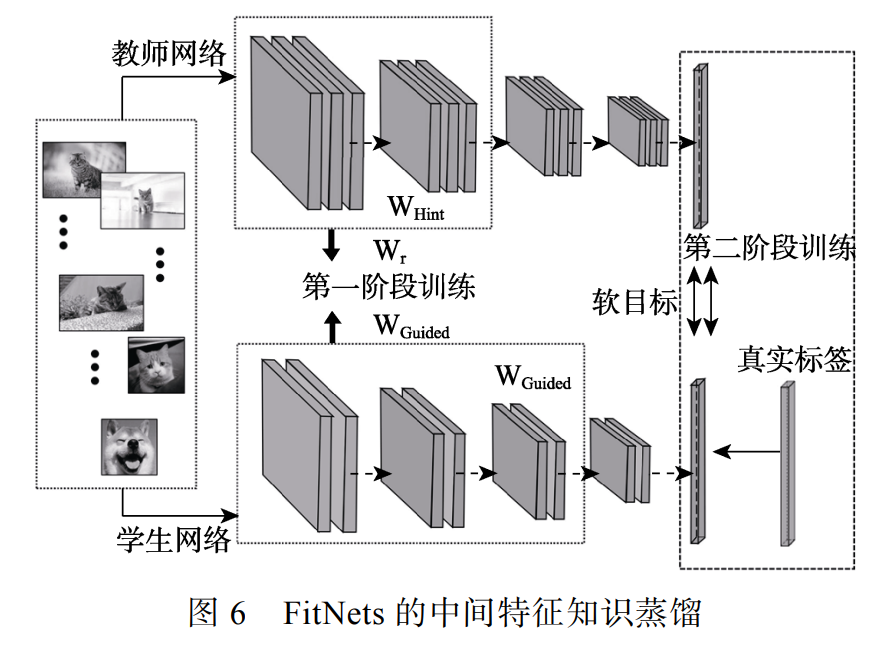
在网络的迁移点上,可以隔层、逐层和逐块地将教师的中间特征知识转移到学生模型中,或者仅迁移教师模型较高隐含层和最后一个卷积层的特征知识。
中间特征的知识蒸馏是要最小化师生之间的中间特征映射距离。这一目标与度量学习的思想很相似。知识蒸馏中应用最广的度量学习算法是 KL散度 。
关系特征知识
关系特征指的是教师模型不同层和不同数据样本之间的关系知识。关系特征知识蒸馏认为学习的本质不是特征输出的结果,而是层与层之间和样本数据之间的关系。
- 基于网络层的关系
- 基于样本间的关系
- 基于相关任务间的关系(特殊任务中)
基于网络层的关系蒸馏(FSP矩阵等)
最早的关系特征知识蒸馏可以追溯到Yim等人的Flow of Solution Procedure(FSP)矩阵,其中通过模仿教师生成的FSP矩阵来实施对学生模型训练的指导。FSP矩阵 $G\in\mathbb{R}^{m\times n}$ 的计算公式为:
\[G_{i,j}(x,W)=\sum_{s=1}^h\sum_{t=1}^w\frac{F_{s,t,i}^1(x,W)\times F_{s,t,j}^2(x,W)}{h\times w}\]其中,$x, W$分别表示输入的图片和权重,$F_{s,t,i}^1和F_{s,t,j}^2$分别表示前一组特征中第$i$个特征图和后一组特征中第$j$个特征图。然后使用$L_2$范数最小化教师与学生的FSP矩阵距离。
\[L_{FSP}(W_t,W_s)=\frac{1}{N}\sum_x\sum_{i=1}^n\lambda\Vert G_i^T(x,W_t)-G_i^S(x,W_s)\Vert_2^2\]其中,$N$表示样本数量,$\lambda_i$表示师生间每一个特征对损失函数的权重,而$T$和$S$分别代表了教师和学生模型。
在Yim等人的工作中,学生模型的训练分为两阶段:
- 最小化师生间的FSP距离矩阵,目的是让学生学到教师模型层之间的关系知识。
- 使用正常的分类损失来优化学生模型。
FSP偏向于测量网络间的关系特征,其局限性在于要求网络的中间层具有相同大小和数量的过滤器,当师生网络层的维度不同时,该方法不能用于表示学习。为了探索不同架构网络层的内部关系,类似捕获网络映射相似性的雅可比矩阵和使用径向基函数计算层间的相关性。
TODO: 雅可比矩阵 和 径向基函数 的用法可以后续仔细读一读然后总结一下。
基于样本间的关系特征知识
该知识同样存在于教师模型的空间结构中。基于样本间的关系特征知识蒸馏是额外利用了不同样本之间的关系知识,即把教师模型捕捉到的数据内部关系迁移到学生模型中。
“学习排名”(Learning to rank)算法是该方法中较早的工作。原理:将知识蒸馏形式化为师生网络之间样本相似性的排列匹配问题,提出利用不同样本之间的关系,并传递交叉样本的相似性知识来改善学生模型。
除了样本间相似性知识之外,关系蒸馏还可以利用相互关系知识和相关性知识。
结构特征知识
结构特征知识是教师模型的完整知识体系,不仅包括教师的输出特征知识,中间特征知识和关系特征知识,还包括教师模型的区域特征分布等知识。
网络性能不仅取决于网路的参数或关系,而且还取决于它的体系结构。结构特征知识蒸馏是以互补的形式利用多种知识来促使学生的预测能包含和教师一样丰富的结构知识。
知识蒸馏的方法
- 知识合并(Knowledge Amalgamation):将多个教师或多个任务的知识迁移到单个学生模型中,从而使其可以同时处理多个任务。一种方法是将多个教师模型的特征知识进行融合;另一种方法是学生模型同时向多个教师模型学习多个任务的特征(选择性学习、共享网络层等)。
- 多教师学习:提高学生模型在单个任务上的性能,学生模型利用教师模型对目标任务的看法(views)来提高模型的性能。我们可以仅使用多个教师的软目标来提高单个学生模型的性能(随机选择一位教师模型的软目标或者通过动态权重选择高效教师模型的软目标);也可同时利用多个教师模型的中间特征知识(投票策略、平均权重和非线性变化等)。也有一些工作特别强调各个教师模型间知识的互补性,同时,向单个教师模型输入具有互补性特征的样本也能充当多教师模型。
- 教师助理(Teacher Assistant)协助学生模型学习。处理的是教师和学生模型由于容量差异大而导致代沟存在的问题。教师助理的选择有很多:GAN(将学生模型当作生成器,判别器促使学生模型对输入数据生成和教师模型同样的特征分布);中等规模的网络(规模介于教师和学生之间,教师助理先从教师模型中学习到知识后,在传递到学生模型中)。上述两种教师助理的选择都使用了教师模型的软目标,同样,我们可以利用异构教师模型的中间特征,允许教师和学生在网络层之间进行直接而有效的一对一匹配来减少代沟问题。也可以以互补的方式从教师模型那里获得知识,其中教师助理主要学习教师和学生的残差错误。
- 跨模态蒸馏(Cross Modal Distillation):利用同步的模态信息实现。特别适用于由于成本或隐私等原因无法得到数据多种模态信息的情况。
- 相互蒸馏(Mutual Distillation):让一组未经训练的学生模型同时开始学习。此为一种在线的知识蒸馏,即教师和学生是同时训练并更新的。其意义在于没有强大教师的情况下,学生模型可以通过相互学习的集成预测来提高性能。实际应用中,相互蒸馏不一定要使用多个网络进行相互学习,也可以在同一个网络上以相互学习的方式同时训练多个分支点的特征提取器或分类器,各个分支通过补充多样化的信息来生成推理能力更强的模型。相互蒸馏也可适用于分布式训练算法,加快训练速度的同时也提高模型的精度。
- 终身蒸馏(Lifelong Distillation)。终身蒸馏通过知识蒸馏来保持旧任务和适应新任务的性能,其重点是训练新数据的手如何保持旧任务的性能来减轻灾难性遗忘。Learning without Forgetting 算法。(TODO: 这个算法后续可以研究下,插个眼)
- 自蒸馏(Self Distillation):单个网络同时被用作教师和学生模型,让单个网络模型在自我学习的过程中通过知识蒸馏去提升性能。主要分为两类,一种是使用不同的样本信息进行互相蒸馏;另一种是单个网络的网络层间进行自蒸馏(使用深层网络的特征去知道浅层网络的学习)。(TODO: 这类算法需要后续研究,插个眼)
知识合并和多教师学习的异同
知识合并和多教师学习都是学习多个教师模型的知识,但是它们的目标不一样:知识合并促使学生模型能同时处理多个教师模型原先的任务;多教师学习是提高学生模型在单个任务上的性能。
相互蒸馏
在相互蒸馏中,监督损失用的是交叉熵损失:
\[L_{C_1}=-\sum_{i=1}^N\sum_{m=1}^MI(y_i,m)\log(p_1^m(X_i))\\ I(y_i,m)=\begin{cases} 1&y_i=m\\ 0&y_i\ne m \end{cases}\]KL散度
对于一个KL散度来说,为了促使两个分类器的概率分布能够接近,$p_1$到$p_2$的KL散度为:
\[D_{KL}(p_2\Vert p_1)=\sum_{i=1}^N\sum_{m=1}^Mp_2^m(X_i)\log\frac{p_2^m(X_i)}{p_1^m(X_i)}\]在$D_{KL}(p_2\Vert p_1)$中,$p_1$把$p_2$当作数据的真实概率分布,目的是使用KL散度使$p_1$的分布近似$p_2$的分布。
交叉熵 Cross Entropy
交叉熵 $H(p,q)$ 可用于度量两个概率分布间的差异性信息。
\[H(p,q)=H(p)+D_{KL}(p\Vert q)\]在神经网络中,交叉熵可作为损失函数,$p$表示真实标记的分布,$q$为训练后模型的预测标记分布,交叉熵损失函数可以衡量$p$和$q$的相似性。交叉熵作为损失函数还有一个好处是使用sigmoid函数在梯度下降过程中能避免均方误差损失函数学习速率降低的问题,因为学习速率可以被输出的误差控制。
\[H(p,q)=\sum_xp(x)\log q(x)\]参考
- 黄震华, 杨顺志, 林威, 等. 知识蒸馏研究综述[J]. 计算机学报, 2022, 45(3).
- Hinton G, Vinyals O, Dean J. Distilling the Knowledge in a Neural Network[J]. stat, 2015, 1050: 9.
- Yim J, Joo D, Bae J, et al. A gift from knowledge distillation: Fast optimization, network minimization and transfer learning[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2017: 4133-4141.