LAD and CoLAD. Improving Object Detection by Label Assignment Distillation
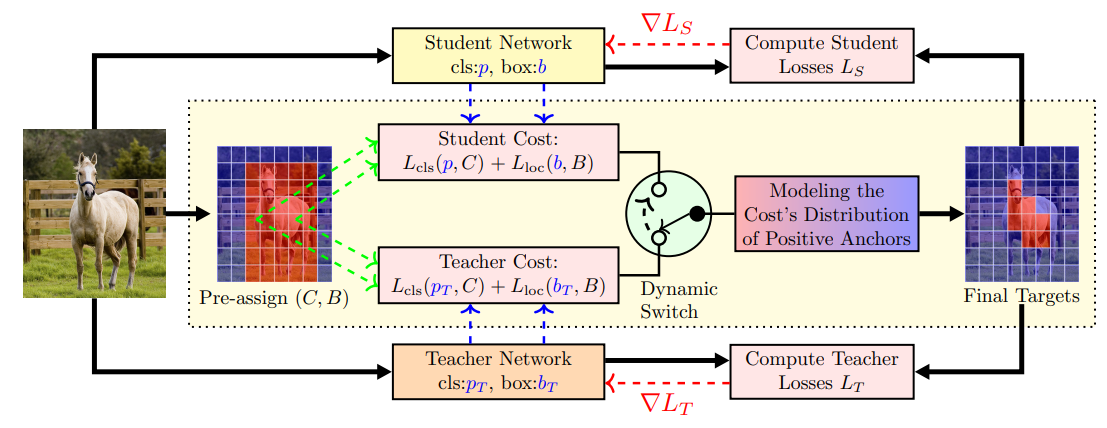
Techniques of label assignment distillation (LAD) and its improved Co-learning version (CoLAD) are introduced in this paper. Change from common versions to LAD is easily implemented by replacing the $(p_i,b_i)$ with the teacher predicts $(p_T^i,b_T^i)$. And the role of teacher or student is decided by the two performance indicators of $\rho_{\sigma/\mu}$ and $\rho_{Fisher}$.
Why label assignment?
- Reviewing the literature, a majority are dedicated to inventing new architectures or defining effective training loss functions. However, the most frontal problem of supervised learning, i.e., how to assign the training targets, yet get less attention, which is orthogonal to previous two ways to improve model performance.
- solely relying on IoU is insufficient, and a combination of classification and localization performance is preferred.
Ironically, a network trained with low IoU assignment yields high recall but noisy predictions, while using only high IoU samples degrades the performance. In addition, regions with the same IoU can have different semantic meaning for classification.
Related works
Label assignment in object detection
Modern object detectors can be single or multi-stages. Single-stage is simpler and more efficient, while multi-stages are more complex but predict with higher precision.
Single stage detectors
In single stage detectors, classification and localization are predicted concurrently for each pixel. There are anchor-based or anchor-free methods. (More can be seen HERE.)
multiple stage detectors
In multi-stage detectors, the first stage network proposes candidate regions, by which the features are cropped and fed to the following stages for the box refinement and class prediction.
Anchor assignments are also different in each stage. In the first stage, i.e. proposal network, an anchor is typically considered as positive if its IoU with any ground-truth is greater than 0.7, negative if less than 0.3, and ignored otherwise. For the second stage, 0.5 IoU threshold is used to separate positive and negative anchors.
Learning label assignment
Learning label assignment approaches update the network weights and learn the assignment iteratively towards final optimization.
Hard assignment
In hard assignment, samples can only be either positive or negative.
- First select and pre-assign a set of potential samples as positive;
- Evaluate their performance by a cost function;
- Finally select a threshold to separate the samples having lower cost as true positive, while the rest are reassigned to negative or ignored.
Soft assignment
In soft assignment, samples can have both positive and negative semantic characteristics. There are two main approaches: soft-weighted loss and soft-targets supervision.
…
Distillation in object detection
Distillation then becomes the principle for many other related problems, such as self-supervised learning.
Applying distillation to object detection is not straightforward, since classification and localization must be learned simultaneously.
LAD extends the distillation concept and is orthogonal with those methods of mimicking the feature, final or intermediate outputs, and using dark knowledge (ability of using dark knowledge uncertainty).
Methods
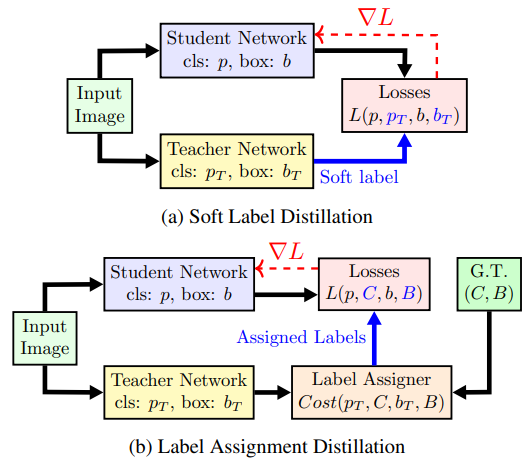
Soft-label distillation
Trick 1: focal term is used to deal with the extreme imbalance problem (introduced before HERE)
\[K L\left(p_{t}, p_{s}\right)=\sum_{c=1}^{C} w^{c}\left(p_{t}^{c} \log \frac{p_{t}^{c}}{p_{s}^{c}}+\left(1-p_{t}^{c}\right) \log \frac{1-p_{t}^{c}}{1-p_{s}^{c}}\right)\tag{1}\]where $p_t, p_s$ denote the teacher and student prediction (i.e. after Sigmoid), $c$ is the class index of total $C$ classes in the dataset, and $w^{c}=\left\vert p_{t}^{c}-p_{s}^{c}\right\vert^{\gamma}$ is the focal term.
replacing the soft-label $p_t$ with an one-hot vector, Equ. (1) becomes the standard Focal loss.
(Alternatively, $\mathcal{L}_1$ and $\mathcal{L}_2$ loss can be also used.)
Different from the classification losses, localization loss is only computed for positive samples. Hence, we select the predicted boxes having $IoU >0.5$ w.r.t. its nearest ground truth box for localization distilling.
Label Assignment Distillation
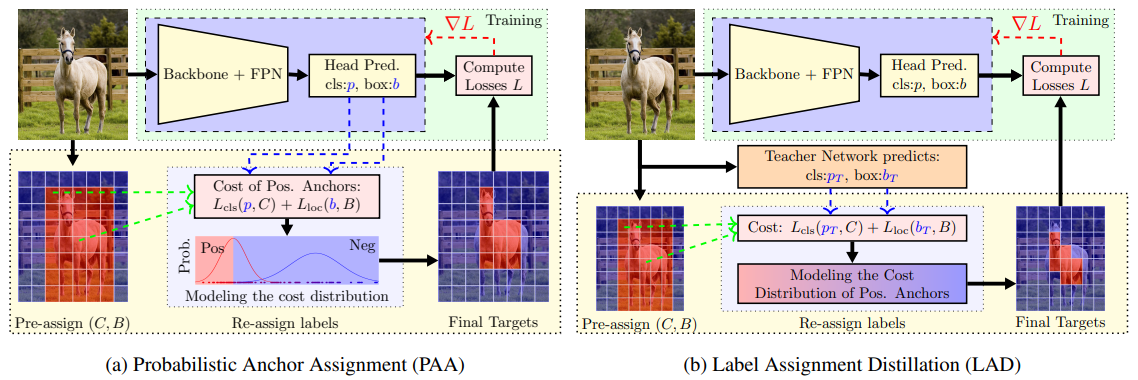
In PAA, for each object, we select a set of anchors ${a_i}$ that have $IoU \ge 0.1$, and evaluate the assignment cost
\[c_{i}=F L\left(p_{i}, C\right)+\left(1-I o U\left(b_{i}, B\right)\right)\tag{2}\]as if they are positive anchors, where $FL$ is the Focal loss, $(p_i, b_i)$ are the predicted class probability and bounding box of $a_i$, $(C, B)$ are the ground truth class and bounding box of the object.
To convert PAA to LAD, we simply use the teacher’s prediction $(p_T^i,b_T^i)$ instead of $(p_i, b_i)$ in Equ. (2).
Co-learning Label Assignment Distillation

This model is easily trapped in the local minima for the reason that the model only exploits the highest short-term reward, i.e. lowest assignment cost, without any chance for exploration.
To tackle the drawbacks of being trapped in local minima and combine the advantages, Co-learning Label Assignment Distillation (CoLAB) is proposed.
We use two separate networks similarly to LAD, but none of them must be pre-trained. Instead, we train them concurrently, and dynamically switch the role of teacher and student based on their performance indicator $\rho$. At each iteration, the network with higher $\rho$ can be selected as the teacher.
Two criteria for $\rho$:
- Std/Mean score $\rho_{\sigma/\mu}$
- Fisher score $\rho_{Fisher}$
In the Fisher Score, we approximate the distribution of ${c_i}$ by a mixture of two Gaussian models $G\left(\mu_{+}, \sigma_{+}\right)+G\left(\mu_{-}, \sigma_{-}\right)$.
Therefore, by dynamically switching the teacher-student, the process no longer relies on a single network, stochastically breaking the loop of training-self assignment. This also brings more randomness at the initial training due to network initialization, hence potentially reducing the risk of local minimal trapping.
Reference
- Nguyen C H, Nguyen T C, Tang T N, et al. Improving object detection by label assignment distillation[C]//Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision. 2022: 1005-1014.